Лекция 3 – Регрессии
8 сентября 2021 г.
📈 Линейная регрессия
Общая форма линейной регрессии
\[ консерватизм = a + b*возраст + \epsilon, \]
\(a\)− константа/свободный член/интерсепт;
- равен среднему значению
y,толькокогда все предикторыxравны нулю, - в остальных случаях имеет только математическую интерпретацию – пересечение с осью
x.
- равен среднему значению
\(b\) − нестандартизованный регрессионный коэффициент при переменной \(возраст\);
- равен разнице значений
yмежду респондентами, которые различаются на 1 единицу поx; - традиционная формулировка “значение возрастания
yпри увеличенииxна единицу” неточна, т.к. никаких изменений (во времени) не происходит.
- равен разнице значений
\(\epsilon\) − дисперсия остатков/случайный член/ошибки.
- “случайный член”, остаточная дисперсия
yне объясненная предикторамиx.
- “случайный член”, остаточная дисперсия
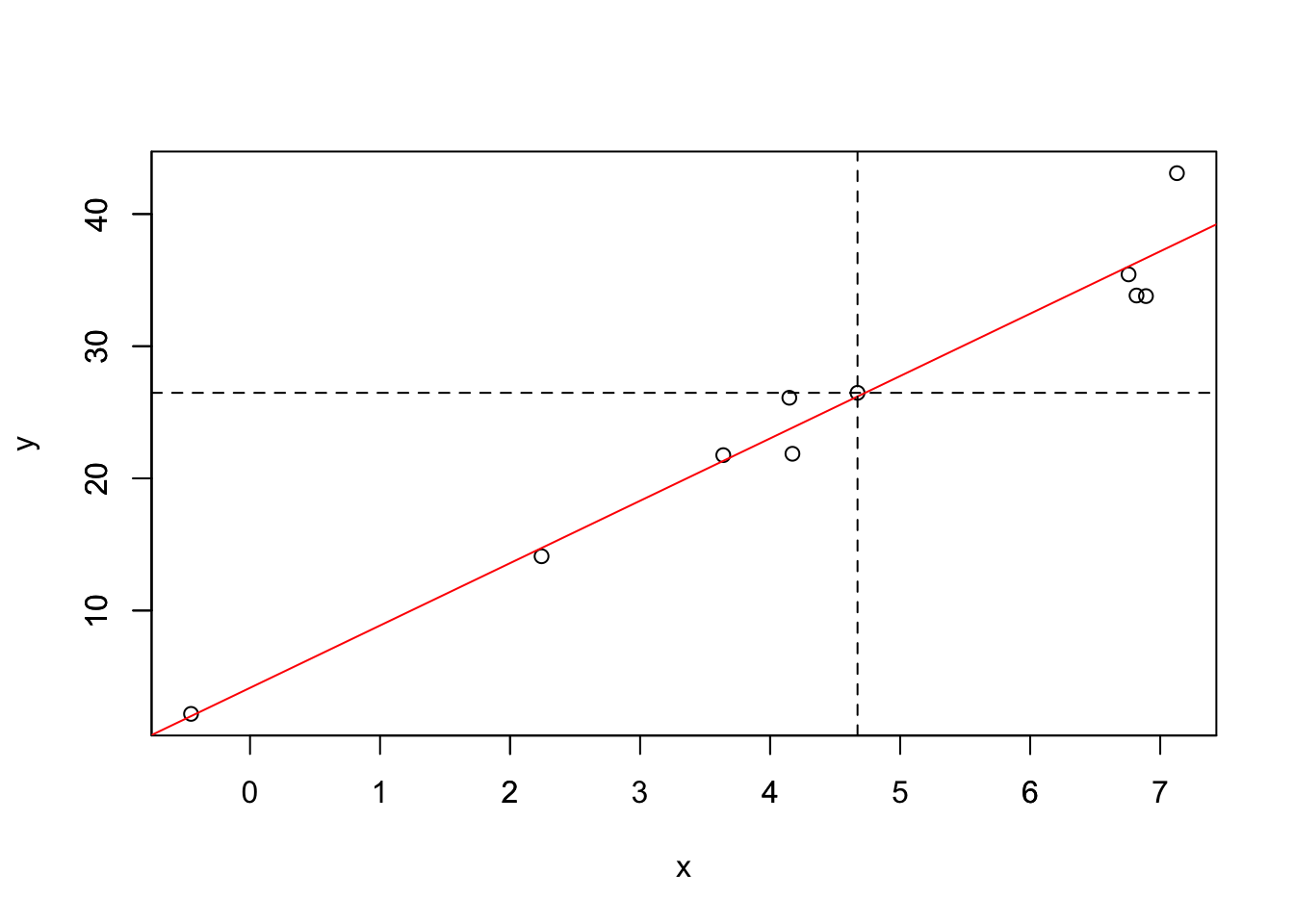
Recap: http://setosa.io/ev/ordinary-least-squares-regression/
Линейные регрессии в R
Функция lm()
Общая форма
fit1 <- lm (
formula = зависимая переменная ~ незаивисимая_переменная1 + незаивисимая_переменная2,
data= файл данных,
subset = отбор_наблюдений,
weights = вес каждого наблюдения,
na.action = na.omit что делать с пропущенными данными
)~ - символ тильда
❗️ Всегда сохраняйте модель в объект, то что выводится в терминале - малая часть информации.
Уровни переменных, дамми-переменные, трансформация
Уровни переменных
Для линейных регрессий зависимая переменная должна быть интервальной. Независимые переменные могут быть любыми, но по-разному вводятся и интерпретируются.
Коэффициенты при дихотомических переменных интерпретируются аналогично интервальным предикторам (см. выше).
Категориальные предикторы вводятся в виде дамми, т.е.
- переменные разбиваются на насколько дихотомических переменных (в соответствии с количеством категорий);
- одна из этих дихотомических переменных исключается из предикторов и выступает “контрольной”/референтной группой;
- коэффициенты остальных дихотомических переменных из этого набора интерпретируются как разница в значениях
yмежду данной группой и контрольной/референтной.
Пример
Зависимая переменная - количество выпитого алкоголя в течение уикэнда.
| Model 1 | |
|---|---|
| (Intercept) | 115.75 (8.13)*** |
| agea | -0.45 (0.07)*** |
| gndr | -19.25 (2.35)*** |
| eduyrs | -1.18 (0.38)** |
| domicil_Suburbs or outskirts of big city | -7.41 (4.08) |
| domicil_Town or small city | -9.94 (3.58)** |
| domicil_Country village | -8.36 (3.42)* |
| domicil_Farm or home in countryside | -13.95 (4.99)** |
| R2 | 0.08 |
| Adj. R2 | 0.08 |
| Num. obs. | 1370 |
| p < 0.001; p < 0.01; p < 0.05 | |
Трансформация интервальных предикторов
Может быть необходима для поиска нелинейных связей.
степенные функции
- квадрат
xбудет указывать на U-образную связь, отрицательный коэффтиент на ∩-образную; - куб
xуказывает на более сложную форму связи; - процедура Бокса-Кокса, функция
boxcox()из пакетаMASS. Она покажет степень, в которую нужно возвести зависимую переменную для нормализации распределенияy. Ограничение:xдолжен быть > 0.
- квадрат
логарифм – используется для сокращения положительного “хвоста” распределения, часто для дохода, т.к. значимость дополнительного дохода увеличивается с ростом дохода
центрирование – вычитание собственной средней из всех интервальных предикторов; приводит к осмысленному значению константы (и в некоторых случаях более корректным коэффициентам взаимодействия);
стандартизация – центрирование + деление на собственное стандартное отклонение; приводит к стандартизованным регрессионным коэффициентам β. Это более предпочтительный способ получения стандартизованных коэффициентов. Функция
scale().
Стандартизация эффектов (коэффициентов)
\[β = b * (SD_x / SD_y) \] Преимущества:
- можно сравнивать вклад разных предикторов.
Недостатки:
- теряется привязка к исходным шкалам;
- плохо интерпретируются в случае категориальных предикторов.
library(lm.beta)
lm.beta::lm.beta(fit2)>
> Call:
> lm(formula = alcwknd ~ agea + gndr + eduyrs + domicil_, data = ess7.Austria)
>
> Standardized Coefficients::
> (Intercept) agea
> 0.00000000 -0.17546405
> gndr eduyrs
> -0.21334401 -0.08499693
> domicil_Suburbs or outskirts of big city domicil_Town or small city
> -0.05710338 -0.09457184
> domicil_Country village domicil_Farm or home in countryside
> -0.08758500 -0.08410044Cтандартная ошибка коэффициентов
- это (гипотетическое) стандартное отклонение коэффициента
Если бы мы собрали данные заново 100 раз, то каждый раз значение коэффициента было бы разным. Распределение этих значений имеет нормальное распределение. Стандартное отклонение этого распределения является стандартной ошибкой коэффициента.
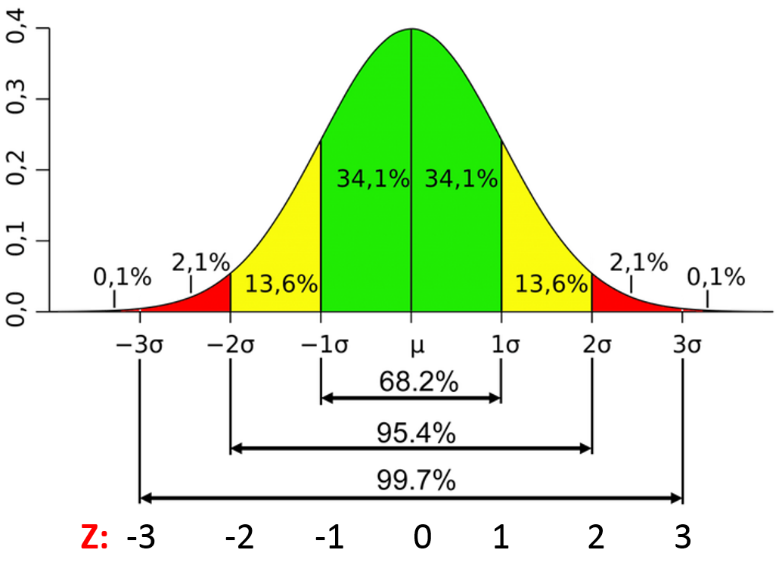
p-значения
На основании стандартной ошибки вычисляются t-значения* (t = нестанд.коэффициент / стандартную ошибку), по которым, в свою очередь, определяется p-значения.
* Иногда используются похожие z-значения.
p-значения подвергаются серьезной критике в последнее время, т.к. зависят от размера выборки (почти всегда низки=значимы на большой выборке), условности пороговых значений (почему именно 0,05?) и теоретической невозможности принять нулевую гипотезу (мы ее “не можем отвергнуть” при определенном p-значении).
Рекомендуется смотреть на более широкий контекст (качество модели в целом, величину стандартизованных коэффициентов, величину эффектов, их содержательную значимость, сравнение разных моделей и т.п.) и осуществлять анализ статистической мощности (power analysis).

\(R^2\)
\(R^2\) - коэффициент множественной корреляции, т.е. корреляция между предсказанной моделью и наблюдаемой переменной, возведенная в квадрат. Доля объясненной дисперсии y.
\(Adj.R^2\) - тот же \(R^2\), но скорректированный на количество предикторов, т.к. количество предикторов само по себе автоматически повышает
Допущения линейных регрессий
Четыре условия Гаусса-Маркова
Все они касаются остатков \(\epsilon\)
1. Средняя равна нулю
(всегда верно если есть константа)
2. Дисперсия остатков постоянна на всех уровнях независимых переменных
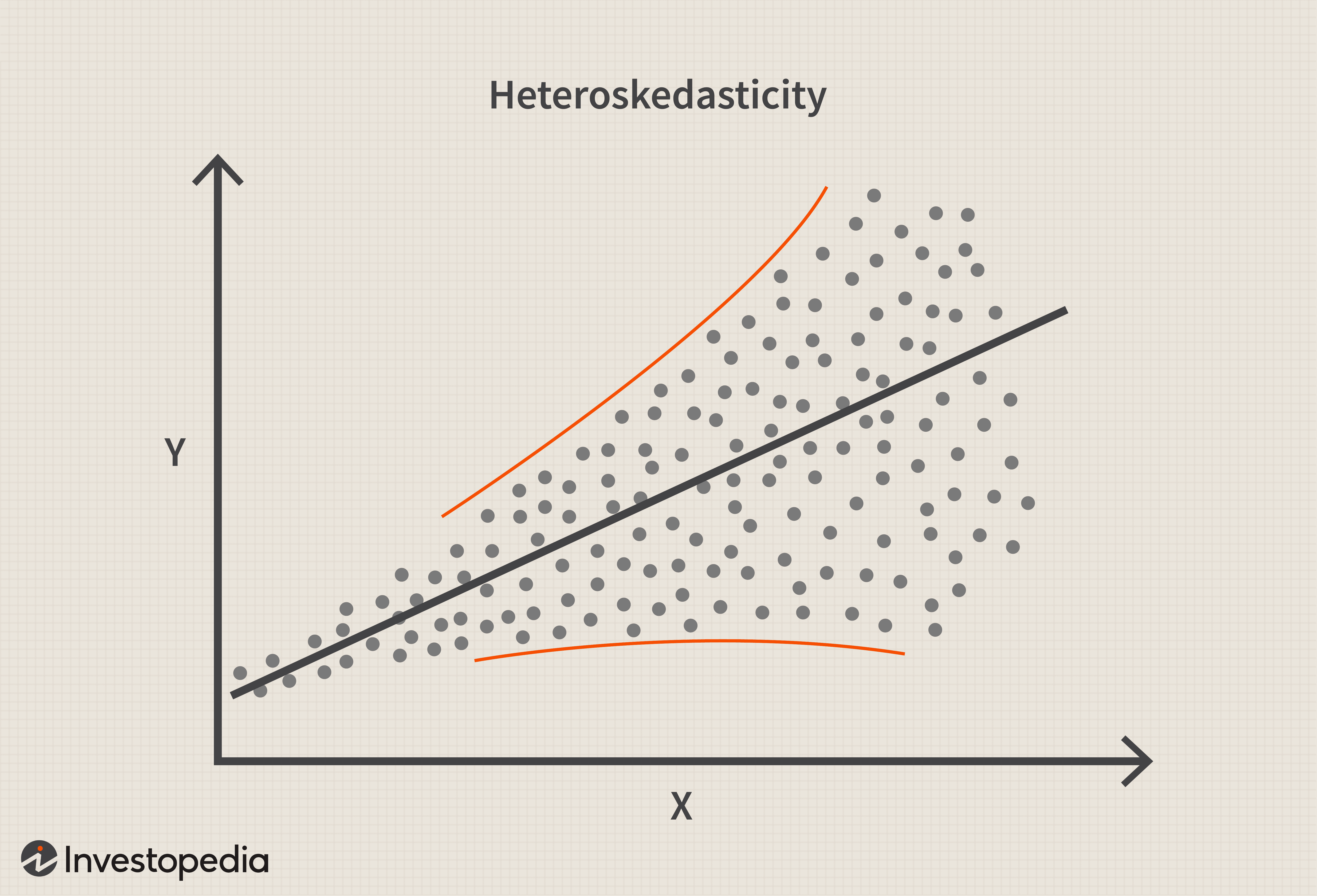
Остатки – гетероскедастичны.
Проблема: Неравномерность распределения остатков по уровням независимой переменной (разные части переменной объясняются моделью с разным успехом).
Последствия: неверные стандартные ошибки (следовательно, значимость коэффициентов).
Диагностика:
- график распределения остатков и предсказанных значений
plot(fit1), - тест Бройша-Пэгана
lmtest::bptest(fit1)или его вариант - NCVcar::ncvTest(fit1)
plot(fit1, 1)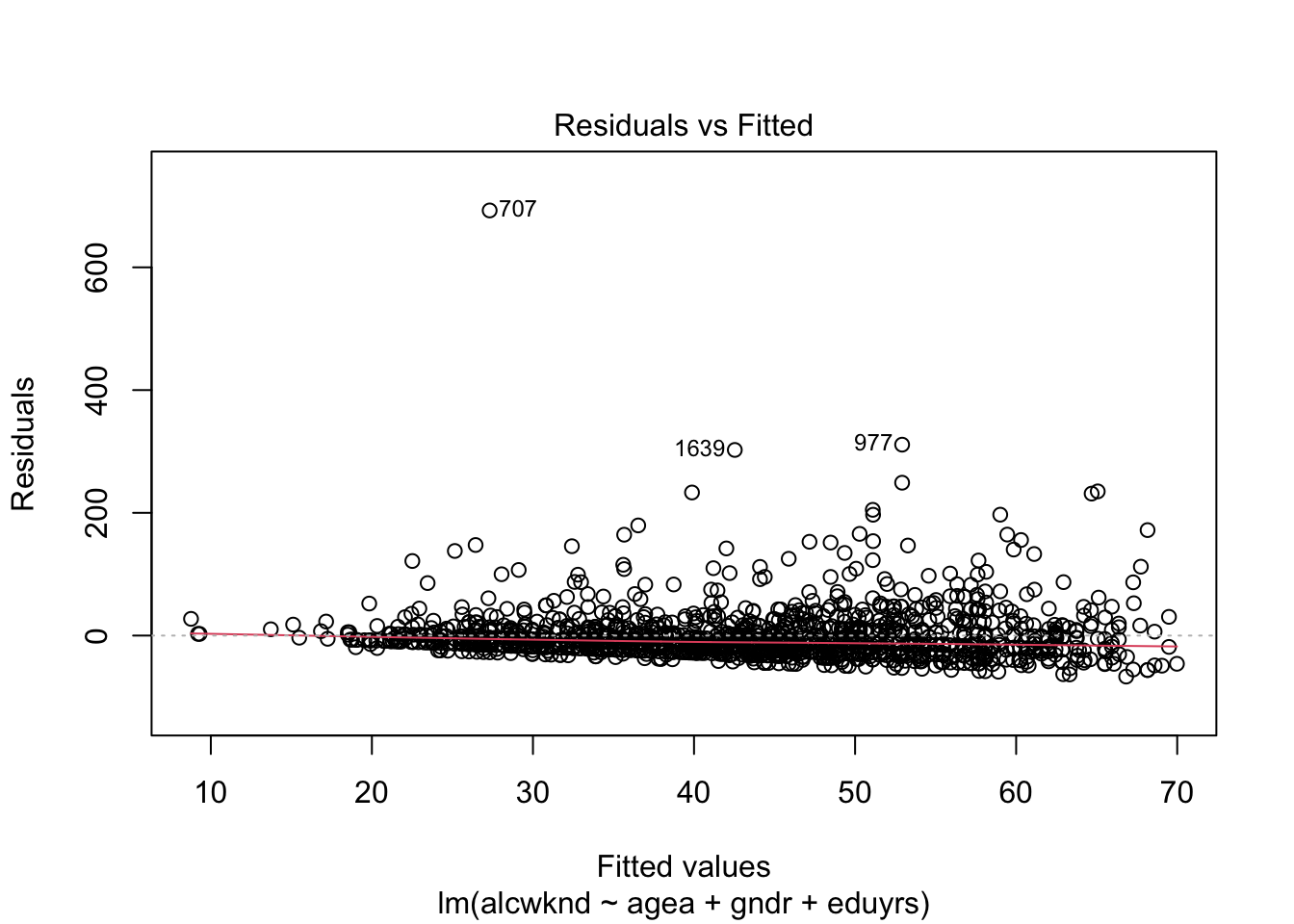
plot(fit1, 3)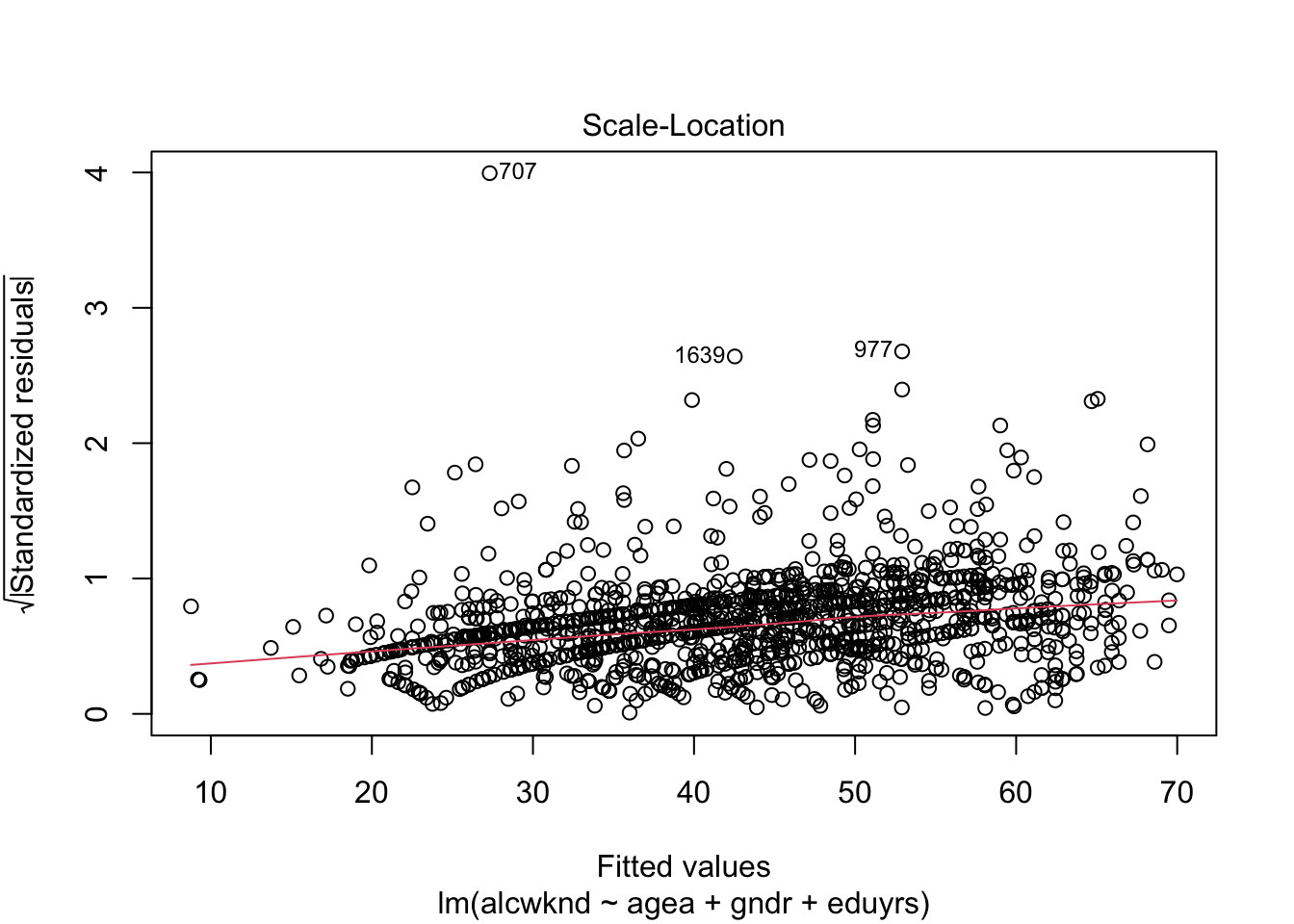
car::spreadLevelPlot(fit1)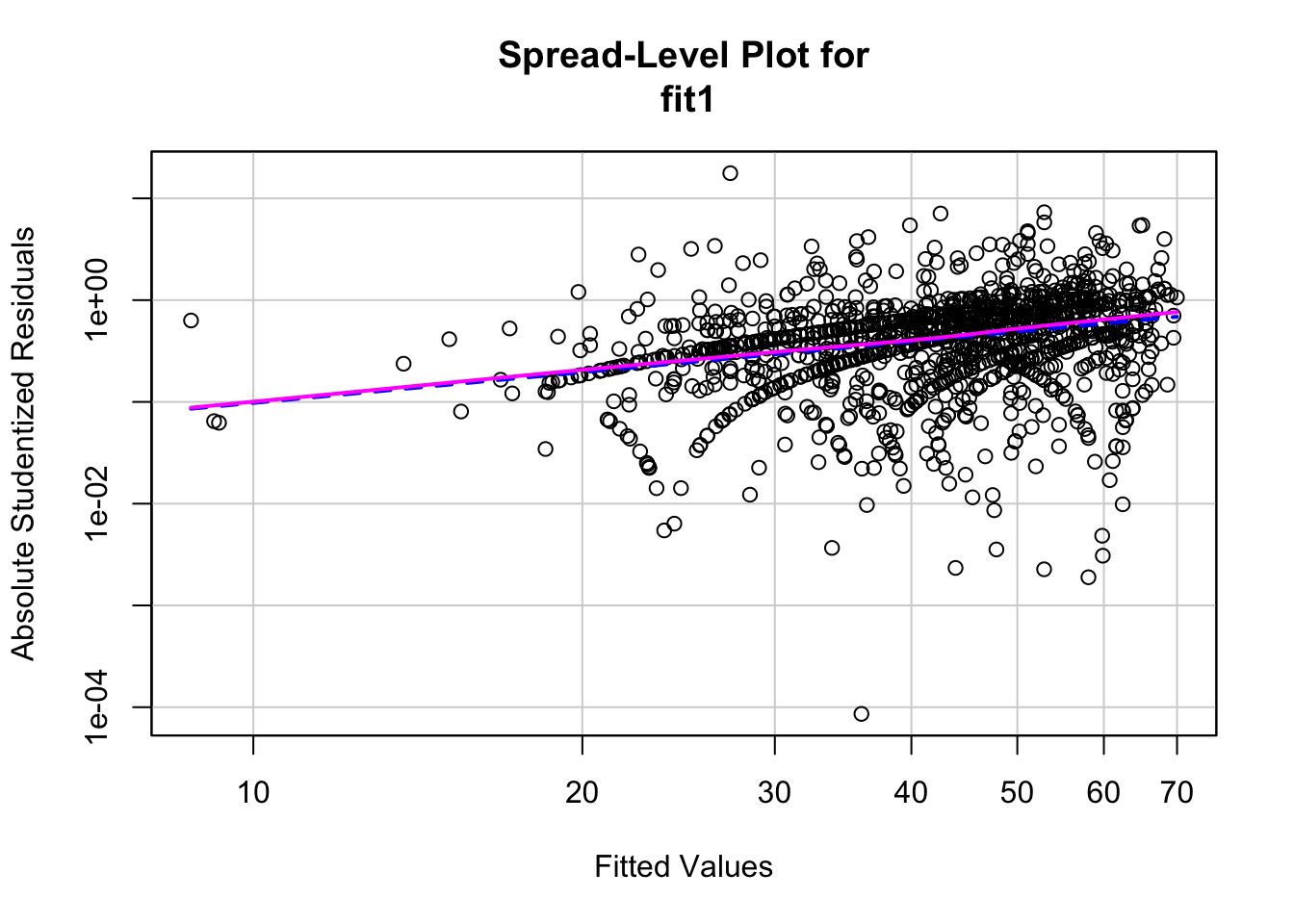
>
> Suggested power transformation: -0.002112601В этих графиках цветные линии должны быть строго горизонтальными. Если есть отклонение от горизонтальности, возможна гетероскедастичность остатков.
3. Остатки независимы друг от друга
Отсутствует автокорреляция (сериальная корреляция). Актуально для моделей включащих временные ряды. Диагностируется критерием Дарбина-Уотсона.
4. Остатки не связаны ни с одной из независимых переменных
Отсутствует проблема эндогенности, то есть корреляции между предикторами и остатками в регрессии.
Источник: пропущенные предикторы, зависимость предиктора от зависимой переменной, проблемы выборки и измерения и т.д.
Остатки распределены нормально
Диагностика: QQ-plot - показывает соответствие распределения остатков теоретическому нормальному распределению. Линия тут – теоретическое ожидание, предсказанное на основе величины дисперсии остатков. Точки - реальные данные. Ожидаем, что все точки лежат на линии.
Тест Шапиро-Вилкса shapiro.test(residuals(fit)) (нулевая гипотеза – распределение нормальное).
См. также - https://xiongge.shinyapps.io/QQplots/
plot(fit1, 2)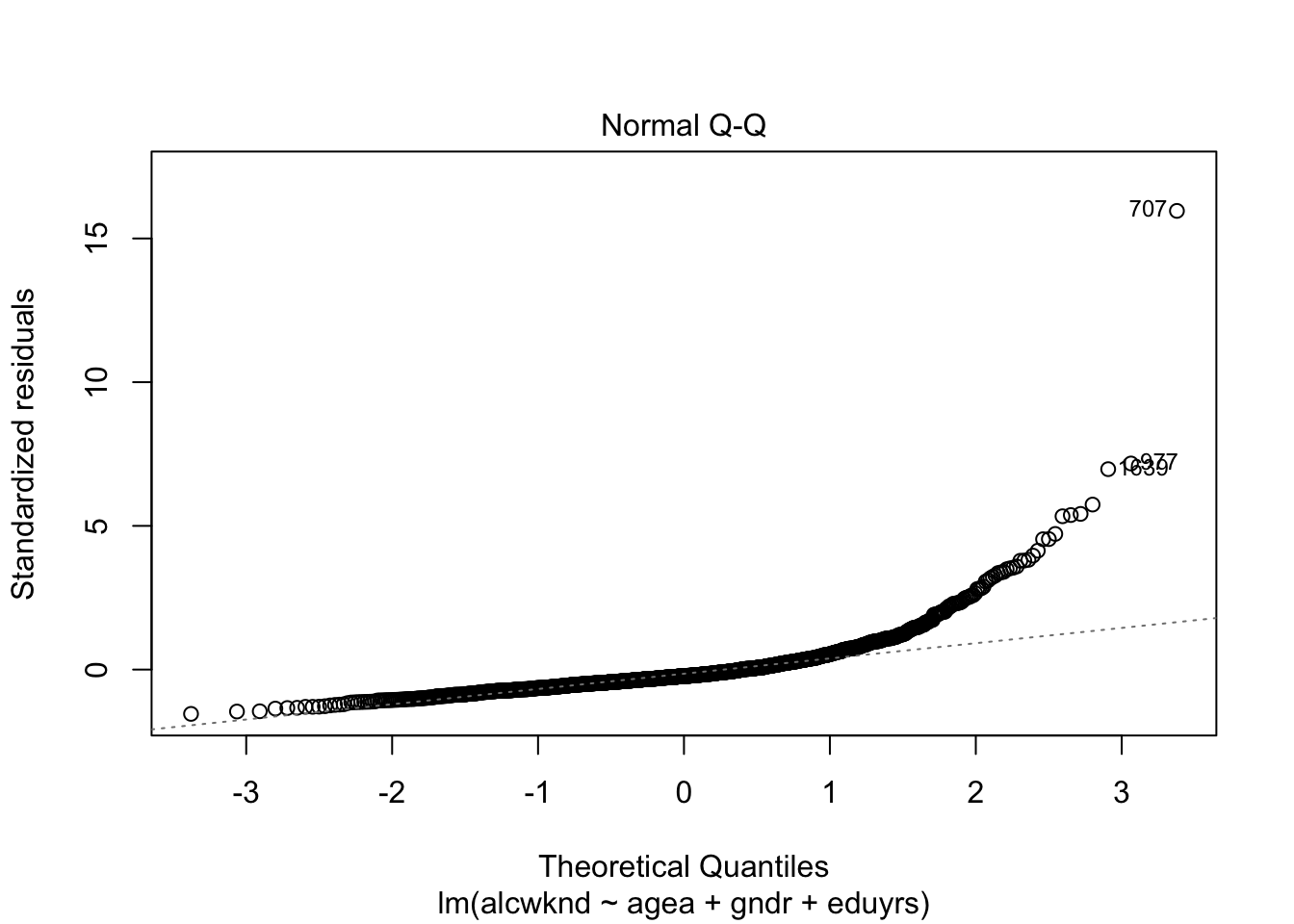
Мультколлинеарность
Невозможность разделить влияние двух предикторов из-за их высокой скоррелированности.
Последствия: неверные стандартные ошибки, нестабильные коэффициенты, но верный \(R^2\).
Диагностика: VIF - variance inflation factor car::vif(fit1) (должен быть <5 или <10).
Работающий пример
alcwknd - количество грамм алкоголя, типично употребляемое по выходным. По-настоящему непрерывная переменная.
fit1 <- lm(alcwknd ~ agea + gndr + eduyrs,
data = ess7.Austria)После того, как модель посчитана, можно применять к ней различные методы, чтобы извлечь необходимую информацию – оценки коэффициентов и показатели качества модели.
summary(fit1)>
> Call:
> lm(formula = alcwknd ~ agea + gndr + eduyrs, data = ess7.Austria)
>
> Residuals:
> Min 1Q Median 3Q Max
> -66.83 -21.80 -9.76 9.29 692.69
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 104.35804 7.21338 14.467 < 2e-16 ***
> agea -0.43648 0.06744 -6.472 1.35e-10 ***
> gndr -19.42131 2.35198 -8.257 3.47e-16 ***
> eduyrs -0.89207 0.36645 -2.434 0.015 *
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Residual standard error: 43.45 on 1367 degrees of freedom
> (424 observations deleted due to missingness)
> Multiple R-squared: 0.07263, Adjusted R-squared: 0.07059
> F-statistic: 35.69 on 3 and 1367 DF, p-value: < 2.2e-16Просмотр результатов
Общая функция для извлечения коэффициентов - coef(), но учтите, что она может работать по-разному (применять разные методы) для результатов разных моделей.
coef(fit1)> (Intercept) agea gndr eduyrs
> 104.3580405 -0.4364807 -19.4213149 -0.8920665Выглядит не очень, но можно быстро привести ее к форме data.frame:
library("texreg")
library("htmltools")
html.tab <- htmlreg(fit1)
browsable(HTML(html.tab))| Model 1 | |
|---|---|
| (Intercept) | 104.36*** |
| (7.21) | |
| agea | -0.44*** |
| (0.07) | |
| gndr | -19.42*** |
| (2.35) | |
| eduyrs | -0.89* |
| (0.37) | |
| R2 | 0.07 |
| Adj. R2 | 0.07 |
| Num. obs. | 1371 |
| p < 0.001; p < 0.01; p < 0.05 | |
Создать регрессионное уравнение на основе объекта
library("equatiomatic")
extract_eq(fit1)\[ \operatorname{alcwknd} = \alpha + \beta_{1}(\operatorname{agea}) + \beta_{2}(\operatorname{gndr}) + \beta_{3}(\operatorname{eduyrs}) + \epsilon \]
Изменим модель
Добавим дополнительный предиктор icpart1 - живет ли респондент с партнером (женой, мужем, вне зависимости от регистрации? обратная кодировка).
fit2 <- lm(alcwknd ~ agea + gndr + eduyrs + icpart1,
data = ess7.Austria)
summary(fit2)>
> Call:
> lm(formula = alcwknd ~ agea + gndr + eduyrs + icpart1, data = ess7.Austria)
>
> Residuals:
> Min 1Q Median 3Q Max
> -65.59 -21.90 -9.84 8.37 689.90
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 96.25409 8.15283 11.806 < 2e-16 ***
> agea -0.41553 0.06814 -6.098 1.4e-09 ***
> gndr -19.70020 2.36282 -8.338 < 2e-16 ***
> eduyrs -0.87274 0.36616 -2.383 0.0173 *
> icpart1 4.94898 2.39896 2.063 0.0393 *
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Residual standard error: 43.34 on 1358 degrees of freedom
> (432 observations deleted due to missingness)
> Multiple R-squared: 0.07464, Adjusted R-squared: 0.07192
> F-statistic: 27.38 on 4 and 1358 DF, p-value: < 2.2e-16Визуализация эффектов
library("sjPlot")
plot_model(fit2, type = "est")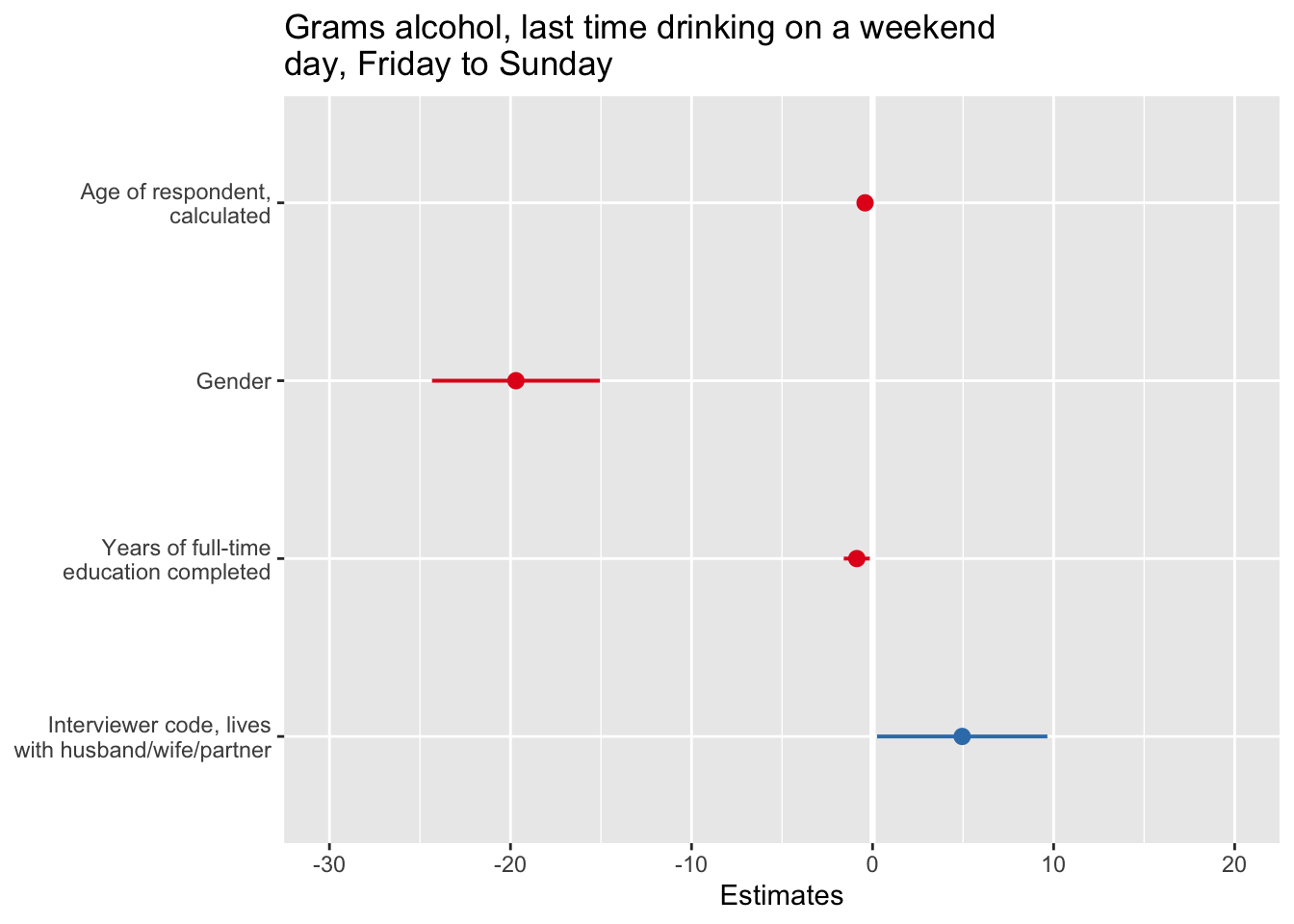
plot_model(fit2, type = "slope", terms = c("agea"))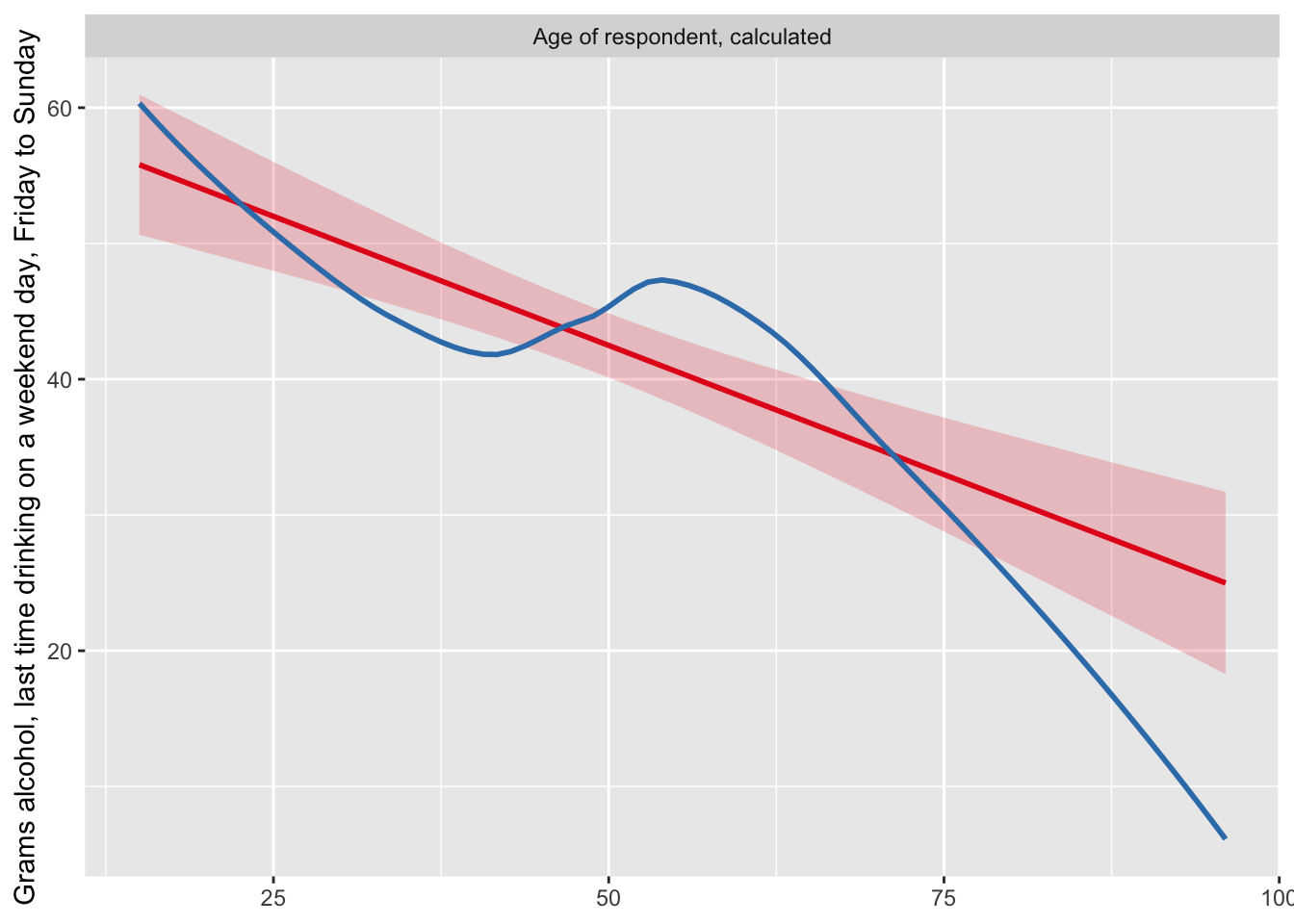
Добавление интеракции (взаимодействия предикторов)
Нелинейные связи и интеракции - http://apps.maksimrudnev.com/learn/paradox.Rmd
female*eduyrs или female + eduyrs + female:eduyrs
fit3 <- lm(alcwknd ~ agea + gndr + eduyrs + icpart1 + eduyrs:gndr,
data=ess7.Austria)
summary(fit3)>
> Call:
> lm(formula = alcwknd ~ agea + gndr + eduyrs + icpart1 + eduyrs:gndr,
> data = ess7.Austria)
>
> Residuals:
> Min 1Q Median 3Q Max
> -65.87 -21.96 -9.86 8.40 690.21
>
> Coefficients:
> Estimate Std. Error t value Pr(>|t|)
> (Intercept) 118.93143 15.39863 7.724 2.19e-14 ***
> agea -0.41094 0.06814 -6.031 2.10e-09 ***
> gndr -35.60164 9.46198 -3.763 0.000175 ***
> eduyrs -2.69715 1.11311 -2.423 0.015520 *
> icpart1 5.02454 2.39758 2.096 0.036296 *
> gndr:eduyrs 1.26099 0.72660 1.735 0.082886 .
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Residual standard error: 43.31 on 1357 degrees of freedom
> (432 observations deleted due to missingness)
> Multiple R-squared: 0.07669, Adjusted R-squared: 0.07329
> F-statistic: 22.54 on 5 and 1357 DF, p-value: < 2.2e-16plot_model(fit3, type = "pred", terms = c("eduyrs", "gndr"))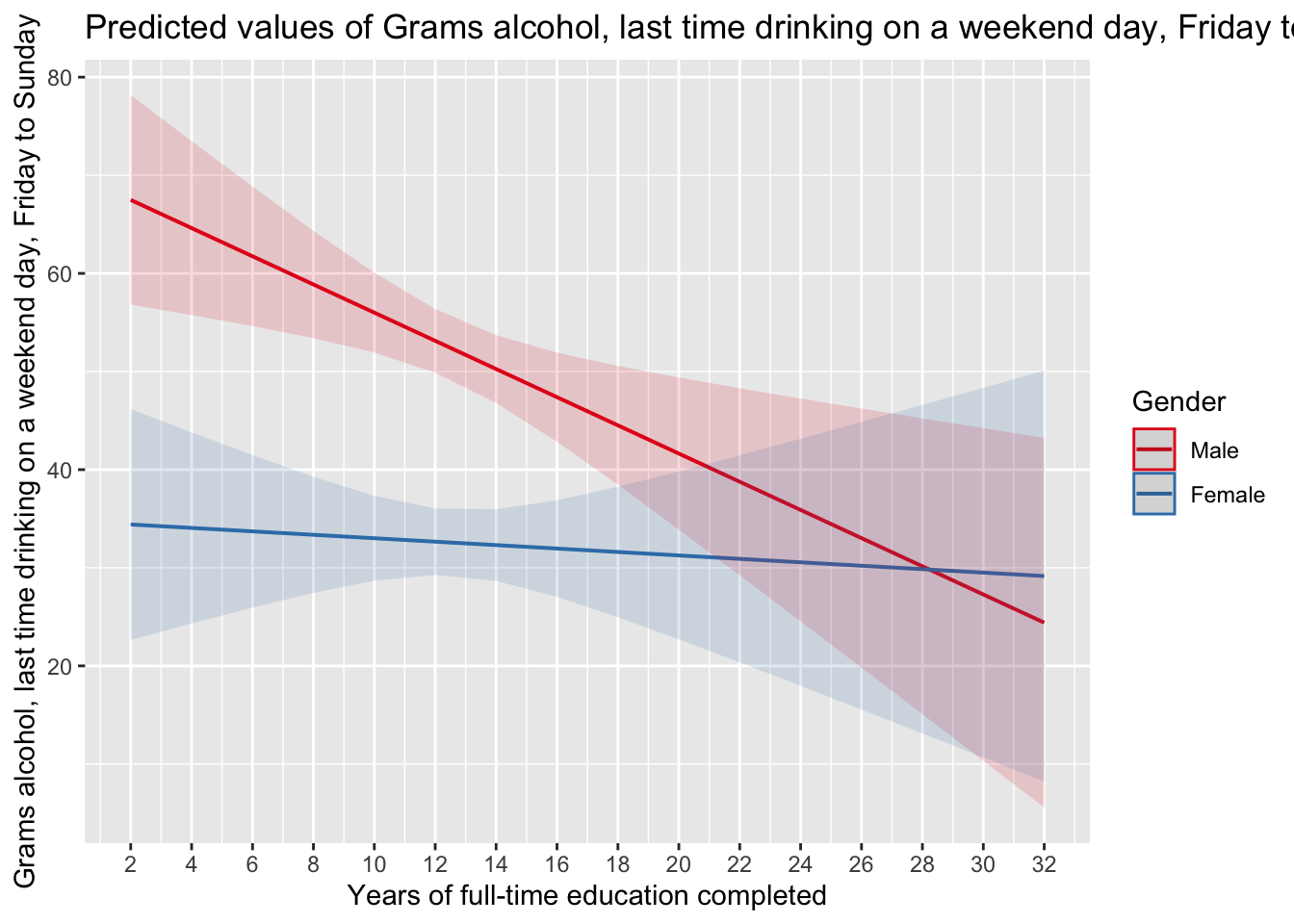
Нелинейные регрессии
Дихотомическая логит/пробит
glm - Generalized Linear Models
ess7.Austria$never <- as.numeric(ess7.Austria$alcfreq == 7) # новая переменная - те, кто сказали что не пили весь год
fit.logit <-
glm(
never ~ agea + gndr + eduyrs, # формула
data=ess7.Austria,
family = binomial(link="logit") # нелинейная функция, связывающая ответы с предикторами
)
summary(fit.logit)>
> Call:
> glm(formula = never ~ agea + gndr + eduyrs, family = binomial(link = "logit"),
> data = ess7.Austria)
>
> Deviance Residuals:
> Min 1Q Median 3Q Max
> -1.0606 -0.8050 -0.5580 -0.4042 2.7308
>
> Coefficients:
> Estimate Std. Error z value Pr(>|z|)
> (Intercept) -1.407909 0.390157 -3.609 0.000308 ***
> agea -0.001471 0.003261 -0.451 0.651878
> gndr 0.951605 0.124198 7.662 1.83e-14 ***
> eduyrs -0.107343 0.021190 -5.066 4.07e-07 ***
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> (Dispersion parameter for binomial family taken to be 1)
>
> Null deviance: 1872.8 on 1771 degrees of freedom
> Residual deviance: 1777.6 on 1768 degrees of freedom
> (23 observations deleted due to missingness)
> AIC: 1785.6
>
> Number of Fisher Scoring iterations: 4Как интерпретируются коэффициенты в бинарной логистической регрессии?
\[ log(\frac{Prob_{never}}{1 - Prob_{never}}) = \beta_0 + \beta_1*Gender + \beta_2*Age + \beta_3Education \]
Порядковая
ess7.Austria$alcfreq.f <- factor(ess7.Austria$alcfreq, ordered=TRUE)
library(MASS)
fit.ordinal1 <-
polr(
alcfreq.f ~ agea + gndr + eduyrs,
data=ess7.Austria,
method = "logistic" # функция, связывающая зависимую с независимыми переменными
)
summary(fit.ordinal1)> Call:
> polr(formula = alcfreq.f ~ agea + gndr + eduyrs, data = ess7.Austria,
> method = "logistic")
>
> Coefficients:
> Value Std. Error t value
> agea -0.01078 0.00241 -4.474
> gndr 1.16396 0.08779 13.258
> eduyrs -0.07175 0.01317 -5.449
>
> Intercepts:
> Value Std. Error t value
> 1|2 -2.3438 0.2729 -8.5870
> 2|3 -0.7107 0.2626 -2.7058
> 3|4 0.2044 0.2625 0.7785
> 4|5 0.7853 0.2633 2.9824
> 5|6 1.1255 0.2640 4.2631
> 6|7 1.7495 0.2659 6.5794
>
> Residual Deviance: 6387.733
> AIC: 6405.733
> (23 observations deleted due to missingness)Вспомним, как интерпретировать коэффициенты из порядковой регрессии.
Альтернативный способ - предсказать вероятности для типичных значений независимых переменных.
predict(fit.ordinal1,
newdata = # создадим фиктивные значения независимых переменных, чтобы предсказать по ним вероятности зависимой
data.frame(
agea=c(20, 30, 40, 50), # разные возрастные группы
gndr= c(1, 1, 1, 1), # мужчины
eduyrs = c(12,12,12,12) # образование примерно среднее
),
type="p")> 1 2 3 4 5 6 7
> 1 0.08082900 0.2296154 0.2187722 0.1385059 0.07076548 0.10203653 0.1594754
> 2 0.08921057 0.2447739 0.2219860 0.1352277 0.06757209 0.09568254 0.1455472
> 3 0.09836826 0.2600136 0.2240217 0.1313227 0.06422612 0.08940412 0.1326435
> 4 0.10835417 0.2751810 0.2248364 0.1268688 0.06077885 0.08325860 0.1207222По строкам тут разные возрастные группы, по столбцам - их вероятность пить с высокой частотой (1) или не пить совсем (7).
Занимательный факт
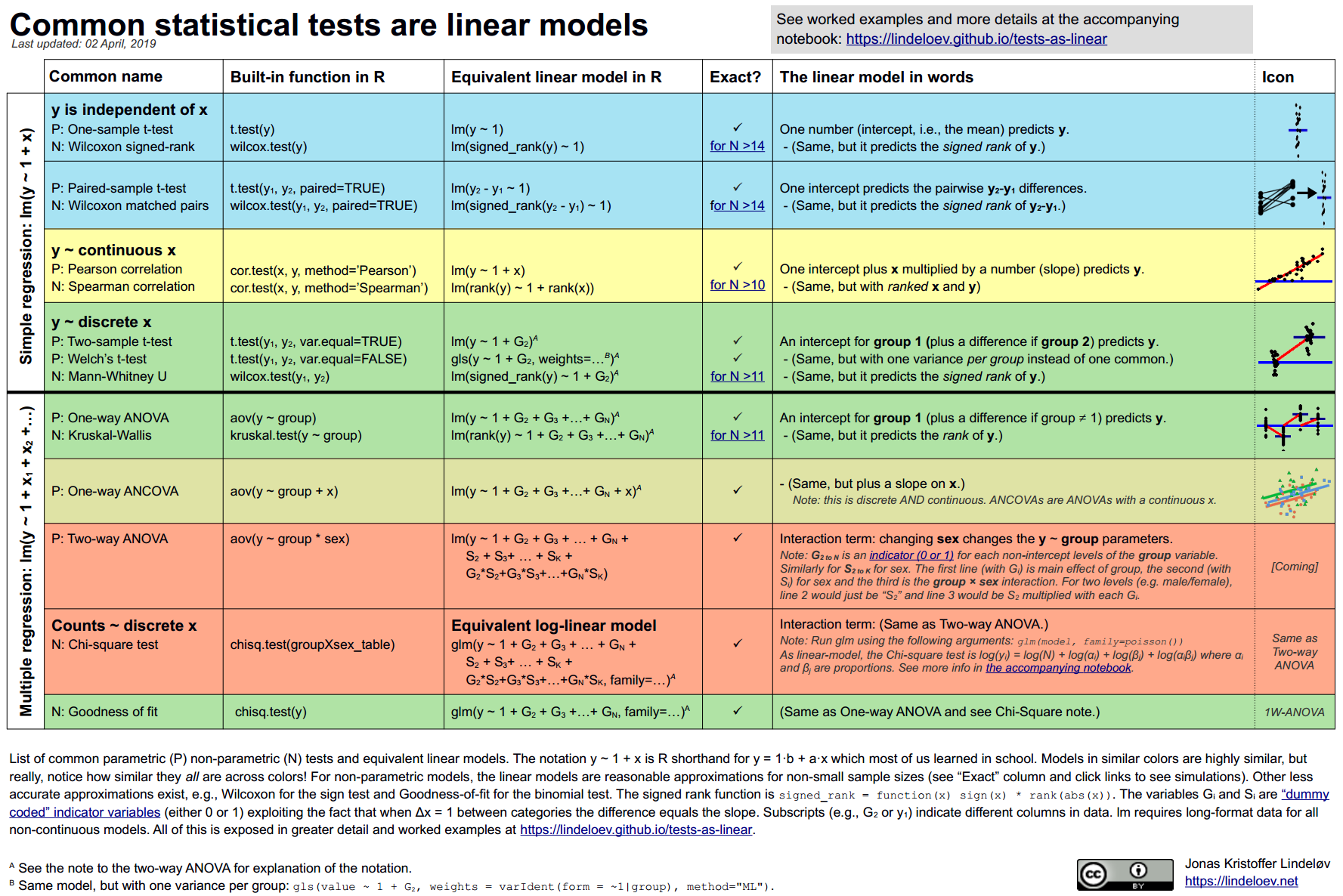
(Почти) Все статистические тесты - это варианты регрессии https://lindeloev.github.io/tests-as-linear/