1 Проекты Rstudio

Rstudio -> File -> New project …

Проекты сохраняют рабочее пространство и автоматически задают рабочую папку. С ними легче следить за версиями скриптов.

2 🖌Описательные статистики

2.1 Таблица сопряженности

  1. Используйте подмассив по Бельгии из прошлого семинара. Если его нет, заново считайте данные ESS-7, оставьте в нем только жителей Бельгии (cntry == "BE"), и перекодируйте переменные domicil и polintr в big.city и polintr.rec.
  2. Посмотрите описательные статистики отдельно по каждой из следующих переменных, используя функцию summary(): polintr.rec, big.city.
  3. Соответствуют ли статистики типам переменных? Если нет, измените эти классы, пересохранив переменные с использованием as.numeric(), as.ordered(), или as.factor().
  4. Постройте таблицу сопряженности политического интереса и размера населенного пункта с помощью функции table().
library(foreign)
mydata <- read.spss(
  file= "data/ESS7e02_1.sav",  # путь к файлу данных
  use.value.labels = F,   # нужно ли использовать ярлыки?
  use.missings = TRUE,         # включать ли пропущенные значения?
  to.data.frame = TRUE       # сформировать из данных data.frame?    
  )


Belgium <- mydata[mydata$cntry=="BE",]

library("car")
Belgium$polintr.rec <- Recode(
  # Переменная, которую нужно перекодировать.
  var = Belgium$polintr,  
  # Перекодировка в формате {входящее значение = исходящее значение}
  recodes = "4=1; 3=2; 2=3; 1=4; else=NA",    
  # Сохранить ли переменную как factor, т.е. номинальную?
  as.factor = FALSE
  )

Belgium$big.city <- Recode(
  var = Belgium$domicil,  # Переменная, которую нужно перекодировать.
  recodes = # Перекодировка в формате {входящее значение = исходящее значение}
    "     1  = 'Большой город';             
      c(2,3) = 'Окраина и небольшой город';  
      c(4,5) = 'Село';
      else=NA
    ",    
  as.factor=TRUE          # Сохранить ли переменную как factor, т.е. номинальную?
  )


summary(Belgium$polintr.rec)
>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
>   1.000   2.000   2.000   2.386   3.000   4.000
summary(Belgium$big.city)
>             Большой город Окраина и небольшой город                      Село 
>                       232                       618                       919
table(Belgium$polintr.rec, Belgium$big.city, useNA = "always")
>       
>        Большой город Окраина и небольшой город Село <NA>
>   1               52                       112  184    0
>   2               83                       194  301    0
>   3               68                       224  363    0
>   4               29                        88   71    0
>   <NA>             0                         0    0    0

2.1.1 Задание

  • Постройте таблицу сопряженности переменных gndr и tvtot функцией table, сохраните ее в объект. Затем подсчитайте проценты по столбцам используя prop.table. Добавьте итоговые строки и колонку функцией addmargins, пересохраните объект с итогами.
  • Округлите результат до двух знаков после запятой, используя функцию round.
tab1 <- table(Belgium$gndr, Belgium$tvtot, useNA="always")
tab2 <- prop.table(tab1, 1)
tab3 <- addmargins(tab2)

round(tab3, 2)
>       
>           0    1    2    3    4    5    6    7 <NA>  Sum
>   1    0.04 0.08 0.15 0.14 0.16 0.17 0.09 0.17 0.00 1.00
>   2    0.03 0.05 0.13 0.17 0.16 0.18 0.10 0.18 0.00 1.00
>   <NA>                                                  
>   Sum

2.2 Меры центральной тенденции

  • Используя функции mean()и sd(), вычислите средние и стандартные отклонения для уровня счастья happy и интереса к политике polintr.rec. 
mean(Belgium$happy, na.rm = T)

mean(Belgium$polintr.rec, na.rm = T)

sd(Belgium$polintr.rec, na.rm  = T)

# sum(Belgium$agea)/length(Belgium$agea)
# 
# sqrt(var(Belgium$agea))

2.3 Статистики по группам

Когда одна из переменных - непрерывная, а вторая - категориальная, полезно смотреть на средние по группам. Для этого пригодны функции by() и aggregate().

by(data = ...,    # переменная по которой будут считаться статистики
   INDICES = ..., # группирующая переменная
   FUN = ...,     # применяемая функция без скобок
   na.rm = ...    # доп.аргументы к применяемой функции
)

2.4 Задание

  • Посчитайте средний интерес к политике в разных типах населенных пунктов, используя функцию by().
  • Посчитайте медианный интерес к политике в разных типах населенных пунктов, используя функцию by().
  • Посчитайте средний интерес к политике в разных типах населенных пунктов с разбивкой по гендеру, используя функцию aggregate(). Обратите внимание, что в качестве группирующей можно использовать сразу несколько переменных.
aggregate(x,      # переменная(ые) для вычисления статистик
          by      # группирующая переменная
          FUN,    # применяемая функция без скобок
          ...     # другие аргументы передаваемые в применяемую функцию 
          )
by(data=Belgium$polintr, # переменная по которой будут считаться статистики
   INDICES=Belgium$gndr, # группирующая переменная
   FUN=mean,             # применяемая функция
   na.rm=TRUE            # аргумент к применяемой функции
)
aggregate(Belgium$polintr.rec, #  переменная(ые) для вычисления статистик
          by=Belgium[, c("big.city", "gndr")],   #  группирующая переменная
          mean,                      # применяемая функция без скобок
          na.rm=TRUE                 # другие аргументы передаваемые в применяемую функцию (в данном случае mean)
          )

3 👭Меры парной связи

3.1 Корреляции

  • Посчитайте корреляцию между интересом к политике и уровнем счастья happy функцией cor(). Первые два аргумента – две переменные для корреляции. Используйте также коэффициент Спирмена (см. help).
  • Посчитайте статистическую значимость этой корреляции используя cor.test().
cor(Belgium$polintr.rec,     # первая переменная
    Belgium$happy,        # первая переменная
    method="pearson",    # коэффициент
    use = "complete"
    )  

cor.test(Belgium$polintr.rec,     # первая переменная
    Belgium$happy,        # первая переменная
    method="pearson",
    use = "complete")

#plot(Belgium$polintr.rec, Belgium$happy)

3.2 Хи-квадрат

Хи-квадрат для таблиц сопряженности вычисляется в два этапа:

  1. Вычиcлить таблицу сопряженности и сохранить ее в объект
  2. Посчитать хи-квадрат функцией chisq.test используя таблицу сопряженности в качестве единственного аргумента.
  • Значимо ли связаны переменные “интерес к политике” и “размер населенного пункта”? Посчитайте хи-квадрат и проинтерпретируйте результаты.
cross.tab <- table(Belgium$polintr.rec, 
                   Belgium$big.city)
chisq.test(cross.tab)

3.3 t-тест

Чтобы посчитать t-тест*, нужно разбить переменную на две группы и “скормить” эти две части переменной функции t.test в качестве первого и второго аргументов.

* - Сравнение двух зависимых выборок можно осуществить, используя аргумент paired = TRUE.

  • Посчитайте t-тест для двух независимых подвыборок голосовавших и неголосовавших (vote) по их интересу к политике.
t.test(
  Belgium$polintr.rec[Belgium$vote==1],  # переменная в первой подвыборке
  Belgium$polintr.rec[Belgium$vote==2]   # переменная во второй подвыборке
  )

Кто проявляет больше интереса к политике - голосовавшие или неголосовавшие?

3.4 Дисперсионный анализ - ANOVA

  • Подсчитывается функцией aov() (Функция anova осуществляет ДРУГОЙ анализ!). Pr(>F) - это значимость f-статистики.
  • Первый аргумент использует формулу в виде
зависимая переменная (интервальная) ~ 
  независимая переменная (категориальная)

Знак ~ это символ тильда.

  • Чтобы увидеть подробные результаты, анализ нужно сохранить в объект и потом извлечь из него информацию функцией summary().

3.5 Задание

  • Проведите дисперсионный анализ, который бы проверял, одинаков ли интерес к политике в населенных пунктах разного размера. Проинтерпретируйте получившийся результат.
  • Дополните анализ контрастами Тьюки - попарными сравнениями с использованием функции TukeyHSD() (единственным аргументом в ней могут быть сохраненные результаты дисперсионного анализа).
  • Различия между средними по группам и их доверительные инетервалы можно легко визуализировать, используя результат функции TukeyHSD() как единственный аргумент в plot().
anova.model1 <- aov(
     formula = polintr.rec ~ big.city, # формула модели, слева от тильды зависимая переменная, справа номинальная независимая.
     data = Belgium
      )
summary(anova.model1)
>               Df Sum Sq Mean Sq F value Pr(>F)  
> big.city       2    6.2  3.1190   3.709 0.0247 *
> Residuals   1766 1485.1  0.8409                 
> ---
> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
TukeyHSD(anova.model1)
>   Tukey multiple comparisons of means
>     95% family-wise confidence level
> 
> Fit: aov(formula = polintr.rec ~ big.city, data = Belgium)
> 
> $big.city
>                                                diff         lwr          upr     p adj
> Окраина и небольшой город-Большой город  0.14705390 -0.01856773  0.312675530 0.0937024
> Село-Большой город                       0.03032719 -0.12771816  0.188372547 0.8943623
> Село-Окраина и небольшой город          -0.11672671 -0.22862688 -0.004826534 0.0385271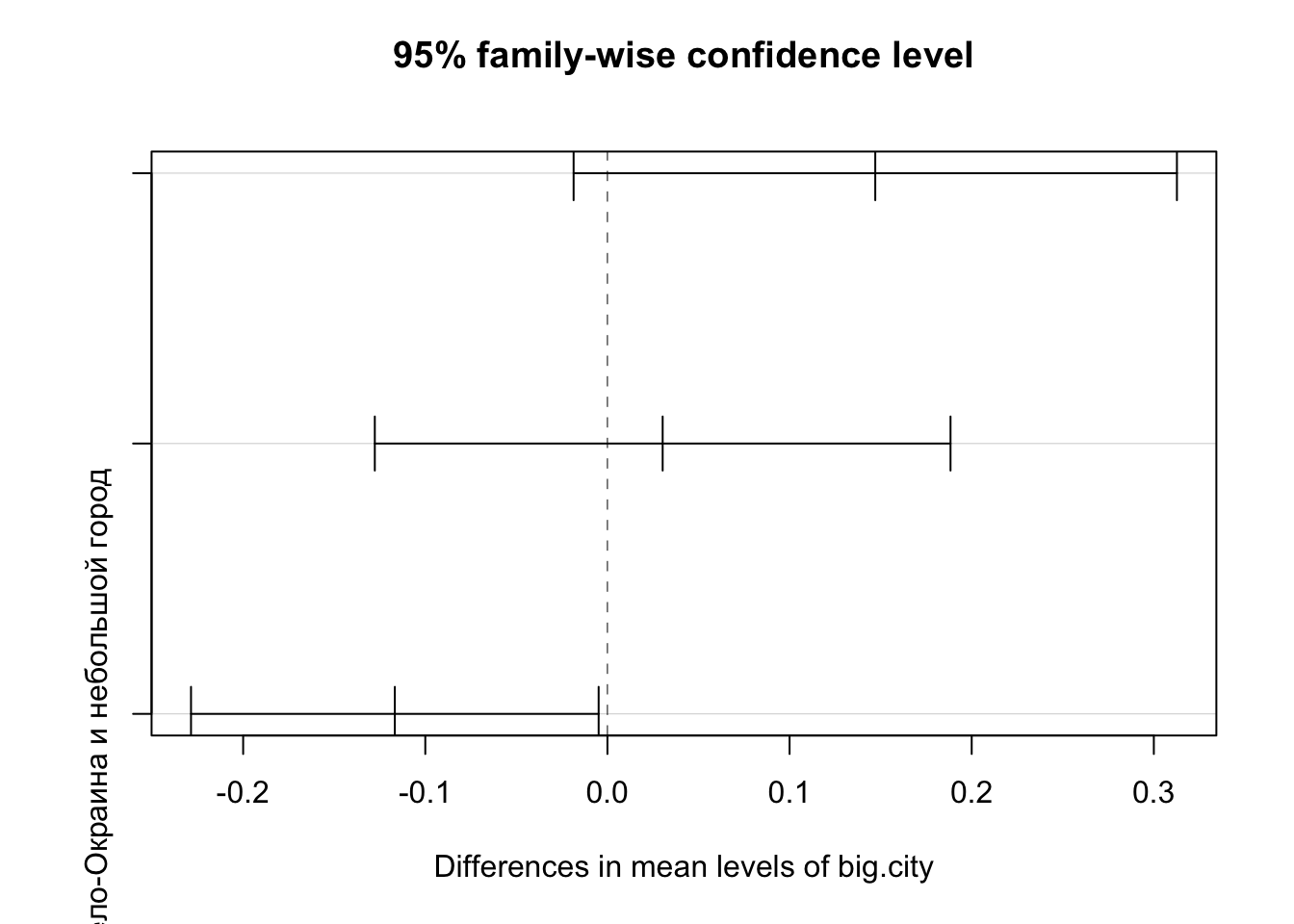
plot(TukeyHSD(anova.model1))

4 📊 Простейшие графики

Попробуйте построить графики, чтобы проиллюстрировать распределения и парные связи

  • Гистограмма hist() для одной интервальной переменной
  • Точечный график scatter.smooth() для двух интервальных переменных
  • “Ящичковый” график boxplot() для одной категориальной и одной интервальной переменной.

5 👉🏻 Большое задание

5.1 Гипотезы

Важность ценности радости и веселья impfun у жителей Швейцарии (код CH в переменной cntry) связана с:

  • полом gndr (мужчины в большей степени склонны разделять ценности свободы),
  • возрастом agea (более молодые люди в большей степени привержены ценности свободы),
  • и образованием eduyrs (более образованные жители Швейцарии сильнее склонны разделять ценность свободы, чем менее образованные),
  • регион, в котором проживает респондент region (жители южных регионов ценят веселье больше). Выясните, какие регионы значимо различаются.

Проверьте эти гипотезы на данных 8 раунда ESS.

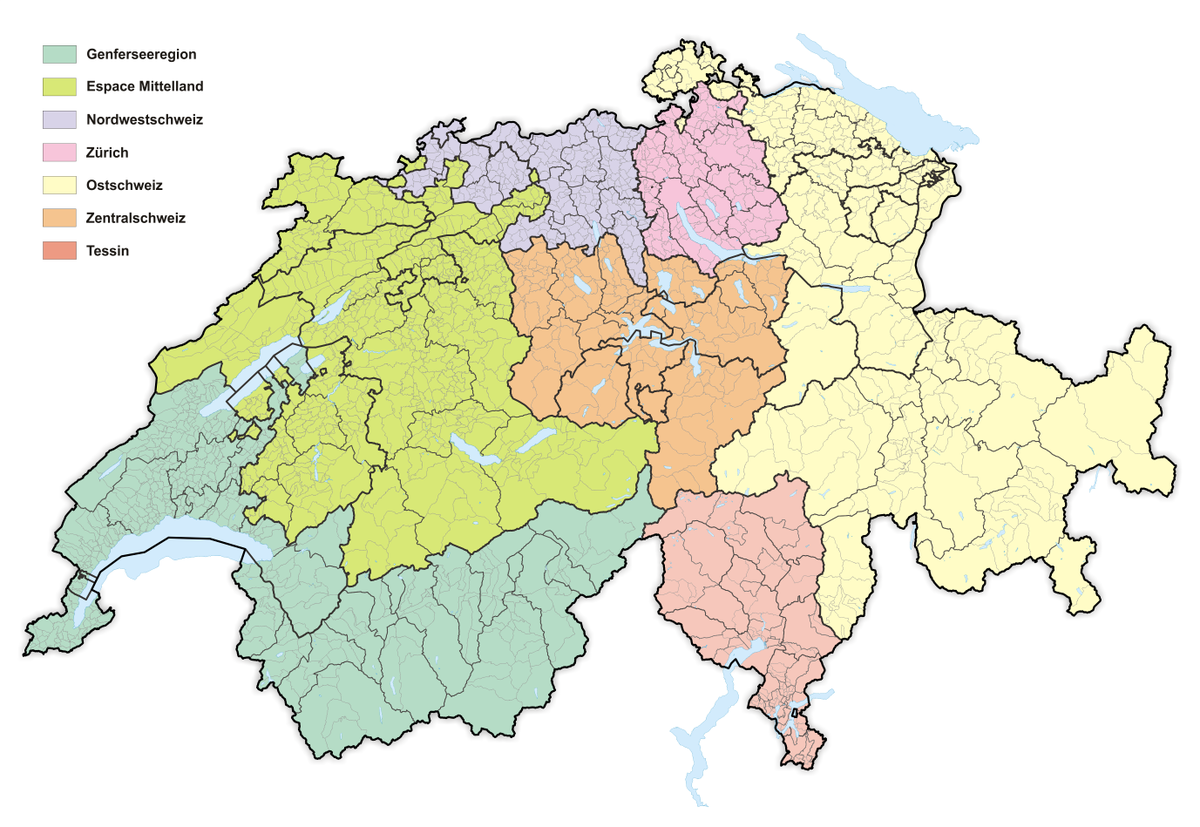https://en.wikipedia.org/wiki/NUTS_statistical_regions_of_Switzerland

d = foreign::read.spss("data/ESS8e02.sav", use.value.labels = F, use.missings = T, to.data.frame = T)

CH <- d[d$cntry=="CH",]

t.test(CH[CH$gndr==1, "impfun"],
       CH[CH$gndr==2, "impfun"])
> 
>   Welch Two Sample t-test
> 
> data:  CH[CH$gndr == 1, "impfun"] and CH[CH$gndr == 2, "impfun"]
> t = -2.1274, df = 1478.1, p-value = 0.03355
> alternative hypothesis: true difference in means is not equal to 0
> 95 percent confidence interval:
>  -0.2689863 -0.0109100
> sample estimates:
> mean of x mean of y 
>  2.763057  2.903005
cor.test(CH$agea,   CH$impfun, method = "spearman")
> 
>   Spearman's rank correlation rho
> 
> data:  CH$agea and CH$impfun
> S = 458641955, p-value = 2.022e-15
> alternative hypothesis: true rho is not equal to 0
> sample estimates:
>       rho 
> 0.2023143
cor.test(CH$eduyrs, CH$impfun, method = "spearman")
> 
>   Spearman's rank correlation rho
> 
> data:  CH$eduyrs and CH$impfun
> S = 551657530, p-value = 0.07213
> alternative hypothesis: true rho is not equal to 0
> sample estimates:
>        rho 
> 0.04623064
ava <- aov(impfun ~ region, CH)

summary(ava)
>               Df Sum Sq Mean Sq F value   Pr(>F)    
> region         6   53.4   8.900   5.548 1.06e-05 ***
> Residuals   1510 2422.1   1.604                     
> ---
> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> 8 observations deleted due to missingness
TukeyHSD(ava)
>   Tukey multiple comparisons of means
>     95% family-wise confidence level
> 
> Fit: aov(formula = impfun ~ region, data = CH)
> 
> $region
>                     diff          lwr         upr     p adj
> CH02 -CH01   0.294216402 -0.008580010  0.59701281 0.0632620
> CH03 -CH01   0.284934655 -0.060344130  0.63021344 0.1841599
> CH04 -CH01   0.415306915  0.079591673  0.75102216 0.0050006
> CH05 -CH01   0.005050505 -0.330664737  0.34076575 1.0000000
> CH06 -CH01   0.202856591 -0.173982145  0.57969533 0.6893326
> CH07 -CH01   0.786796537  0.236691917  1.33690116 0.0005095
> CH03 -CH02  -0.009281748 -0.333299993  0.31473650 1.0000000
> CH04 -CH02   0.121090513 -0.192716925  0.43489795 0.9159118
> CH05 -CH02  -0.289165897 -0.602973335  0.02464154 0.0938543
> CH06 -CH02  -0.091359811 -0.448820043  0.26610042 0.9889726
> CH07 -CH02   0.492580135 -0.044435207  1.02959548 0.0968919
> CH04 -CH03   0.130372261 -0.224602217  0.48534674 0.9328037
> CH05 -CH03  -0.279884150 -0.634858628  0.07509033 0.2312941
> CH06 -CH03  -0.082078063 -0.476171440  0.31201531 0.9963612
> CH07 -CH03   0.501861882 -0.060203283  1.06392705 0.1159819
> CH05 -CH04  -0.410256410 -0.755935691 -0.06457713 0.0085476
> CH06 -CH04  -0.212450324 -0.598192303  0.17329165 0.6654548
> CH07 -CH04   0.371489621 -0.184751814  0.92773106 0.4332286
> CH06 -CH05   0.197806086 -0.187935892  0.58354807 0.7365363
> CH07 -CH05   0.781746032  0.225504596  1.33798747 0.0006968
> CH07 -CH06   0.583939945  0.001954341  1.16592555 0.0485965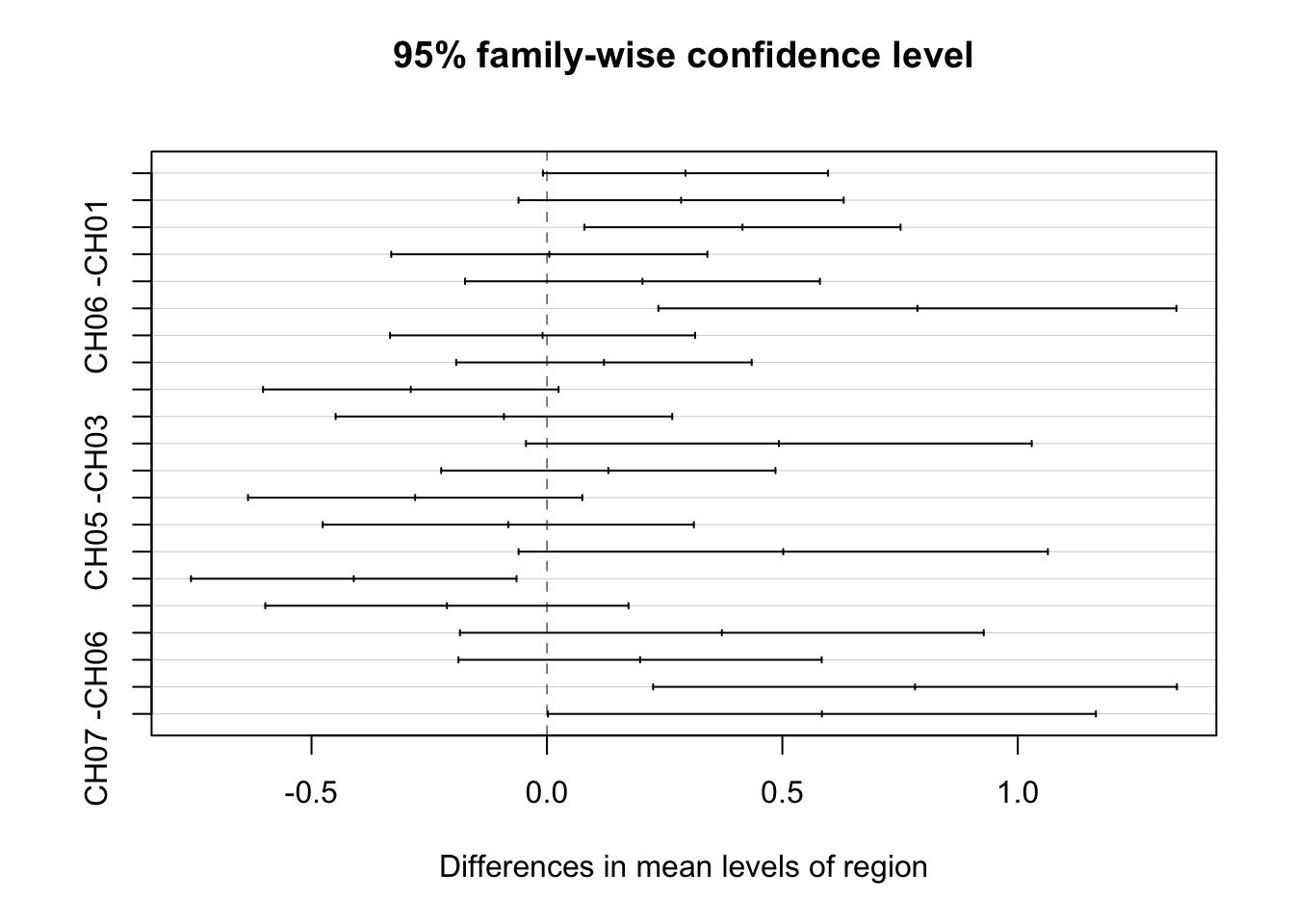
plot(TukeyHSD(ava))

5.2 Составьте план анализа

Продумайте последовательность операций по обработке данных. Обычно они включают: чтение, чистку (фильтрацию, перекодирование), описательную статистику, модели и представление результатов.

  • какой функцией (лучше) считывать данные?
  • какие респонденты нам нужны?
  • какие переменные потребуются?
  • какие показатели парной связи можно использовать для этих переменных?
  • какие функции R подходят для подсчета этих показателей?


Максим Руднев, 2018-2021 на основе RMarkdown.