1 Задание 1 – проверка простых гипотез

См. Работающий пример в Лекции 3

Используя образец из лекции, постройте регрессионную модель, которая проверяла бы те же гипотезы, что и отдельные тесты на прошлом семинаре:

1.1 Гипотезы

Важность ценности веселья impfun у жителей Швейцарии (код CH в переменной cntry) связана с:

полом gndr (мужчины в большей степени склонны разделять ценности веселья),
возрастом agea (более молодые люди в большей степени привержены ценности веселья);
и образованием eduyrs (более образованные жители Швейцарии сильнее склонны разделять ценность веселья, чем менее образованные);
регион, в котором проживает респондент region. Выясните, какие регионы значимо различаются.

Дополнительно: возраст имеет более сильный эффект на ценность веселья, чем образование.

Проверьте эти гипотезы на данных 8 раунда ESS.

# считываем данные
library("foreign")

d <- read.spss("data/ESS8e02.sav", 
               use.value.labels = F, 
               use.missings = T, 
               to.data.frame = T
               )

# отбираем швейцарцев
CH <- d[d$cntry == "CH",]

# меняем кодировку на обратную
CH$impfun.rec <- 7 - CH$impfun

# строим регрессионную модель
fit1 <- lm(impfun.rec ~ gndr + agea + eduyrs + region, CH)

# делаем таблицу регрессионных коэффициентов
library("texreg")
library("htmltools")

htab1 <- htmlreg(fit1)
browsable(HTML(htab1))

Statistical models
	Model 1
(Intercept)	5.63^***
	(0.20)
gndr	-0.12
	(0.06)
agea	-0.01^***
	(0.00)
eduyrs	-0.03^**
	(0.01)
regionCH02	-0.34^***
	(0.10)
regionCH03	-0.34^**
	(0.11)
regionCH04	-0.45^***
	(0.11)
regionCH05	-0.13
	(0.11)
regionCH06	-0.30^*
	(0.13)
regionCH07	-0.78^***
	(0.18)
R²	0.07
Adj. R²	0.06
Num. obs.	1508
^*p < 0.001; ^p < 0.01; ^*p < 0.05

2 Задание 2 – квадратические связи

Стандартизируйте все интервальные переменные в модели и заново вычислите коэффициенты.
Проверьте криволинейный эффект возраста и количества лет образования, дополнив модель их квадратами. Квадраты можно вводить непосредственно в формулу в виде I(predictor).

Обертка I() необходима для правильного считывания формулы, функция I() изолирует выражение и позволяет совершать разные преобразования внутри формулы. Это необходимо для последующего построения графиков.

Если какой-то из квадратических эффектов обнаружится, постройте график, демонстрирующий эту связь, используя функцию plot_model() и аргумент type = "eff".

# вычисляем стандартизованные коэффициенты
fit2 <- lm(scale(impfun.rec) ~ 
             gndr + scale(agea) + scale(eduyrs) +  region, 
           CH
           )

# смотрим на таблицу коэффициентов
htab2 <- htmlreg(fit2)
browsable(HTML(htab2))

Statistical models
	Model 1
(Intercept)	0.37^***
	(0.10)
gndr	-0.10
	(0.05)
scale(agea)	-0.21^***
	(0.03)
scale(eduyrs)	-0.07^**
	(0.03)
regionCH02	-0.27^***
	(0.08)
regionCH03	-0.27^**
	(0.09)
regionCH04	-0.35^***
	(0.09)
regionCH05	-0.10
	(0.09)
regionCH06	-0.24^*
	(0.10)
regionCH07	-0.61^***
	(0.14)
R²	0.07
Adj. R²	0.06
Num. obs.	1508
^*p < 0.001; ^p < 0.01; ^*p < 0.05

# добавили квадратические члены
fit3 <- lm(scale(impfun.rec) ~ 
             gndr + scale(agea)  + I(agea^2) + 
             scale(eduyrs)  + I(eduyrs^2) +  
             region, 
           CH
           )

# смотрим на таблицу коэффициентов
htab3 <- htmlreg(fit3)
browsable(HTML(htab3))

Statistical models
	Model 1
(Intercept)	0.14
	(0.30)
gndr	-0.10
	(0.05)
scale(agea)	-0.50^***
	(0.13)
agea^2	0.00^*
	(0.00)
scale(eduyrs)	0.07
	(0.14)
eduyrs^2	-0.00
	(0.00)
regionCH02	-0.27^***
	(0.08)
regionCH03	-0.27^**
	(0.09)
regionCH04	-0.36^***
	(0.09)
regionCH05	-0.10
	(0.09)
regionCH06	-0.23^*
	(0.10)
regionCH07	-0.62^***
	(0.14)
R²	0.07
Adj. R²	0.07
Num. obs.	1508
^*p < 0.001; ^p < 0.01; ^*p < 0.05

# визуализируем эффект возраста
library("sjPlot")

plot_model(fit3, 
           type = "eff", 
           terms = "agea"
           )

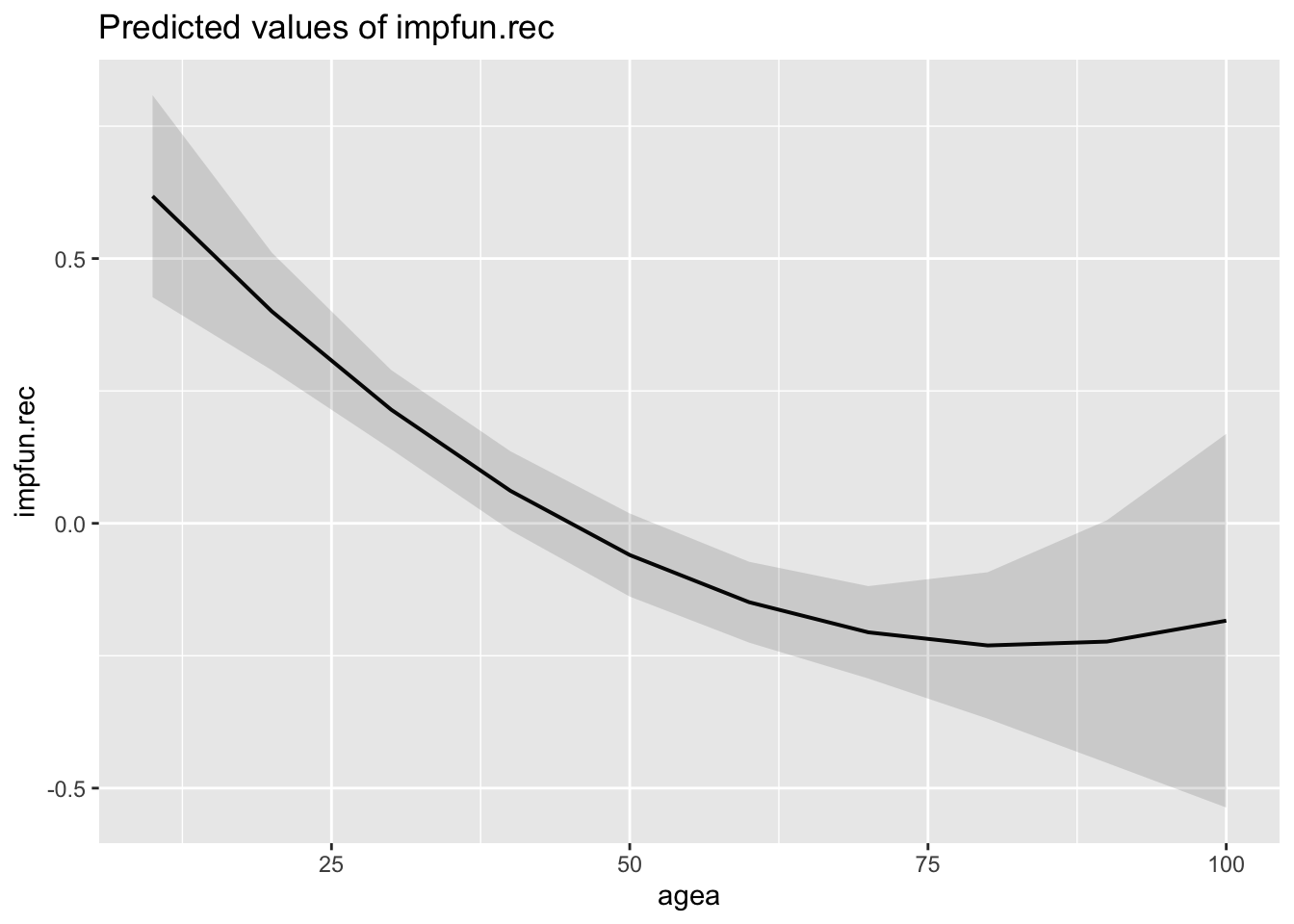
3 Задание 3 – диагностика

Проведите диагностику моделей

высок ли R²?
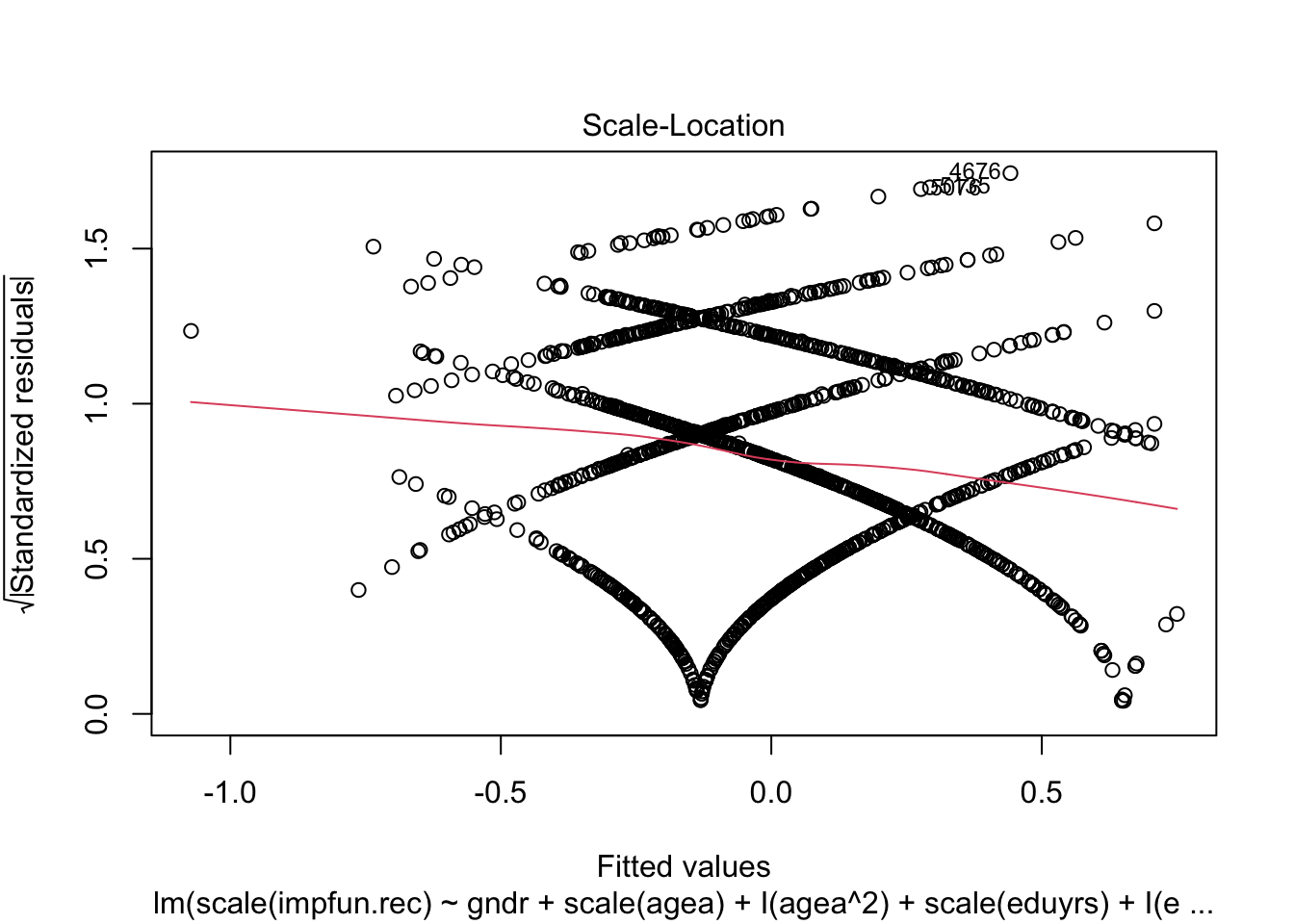
мультиколлинеарность (car::vif(), проблема если >5 или >10);
гомоскедастичность lmtest::bptest() тест Бреуша-Пэгэна, тест непостоянной дисперсии остатков (значимый указывает на наличие гетероскедастичности);
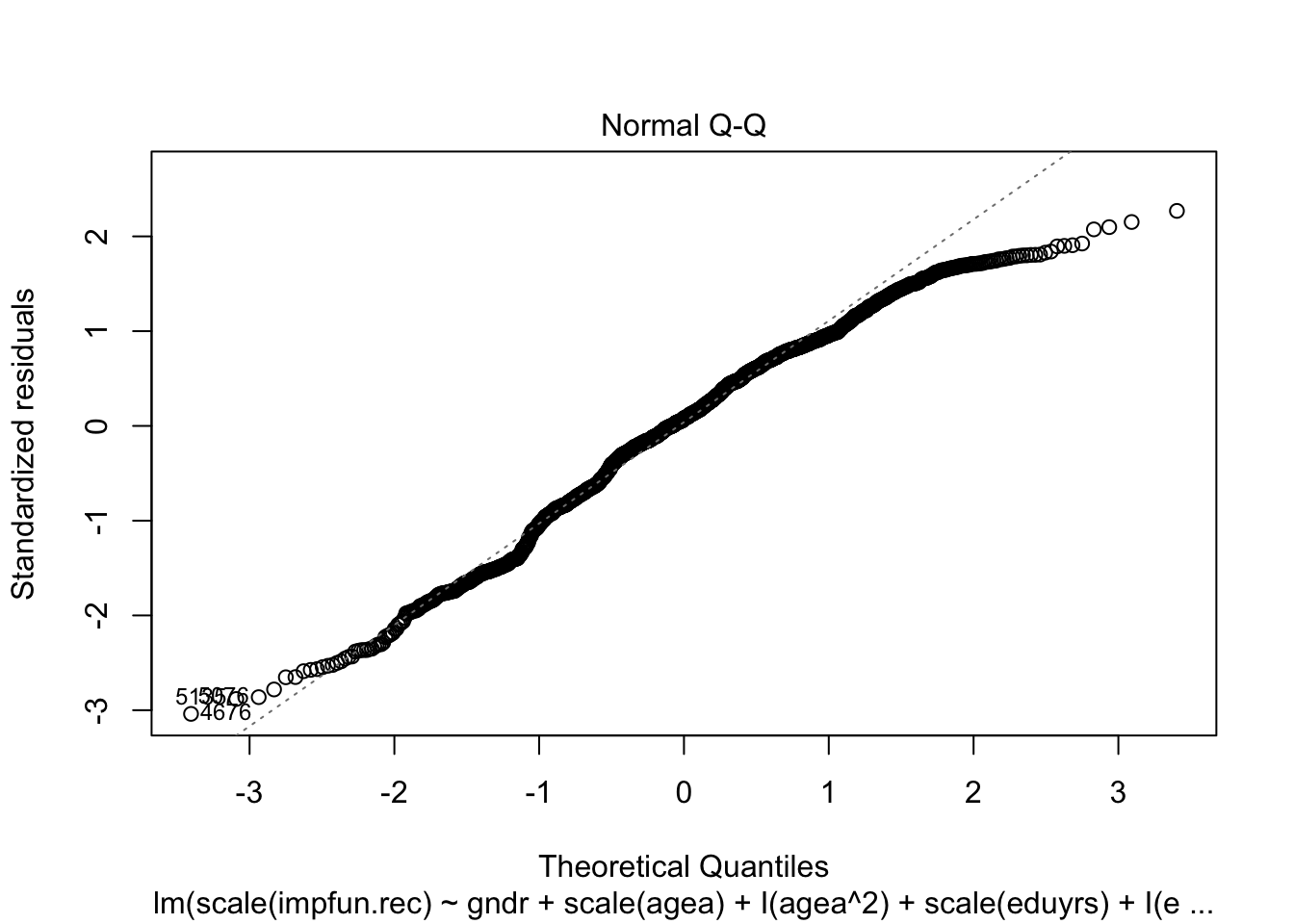
нормальность распределения остатков shapiro.test()
plot() - диагностические графики.

# диагностика по графикам
plot(fit3)

# проверка на мультиколлинеарность
car::vif(fit3)

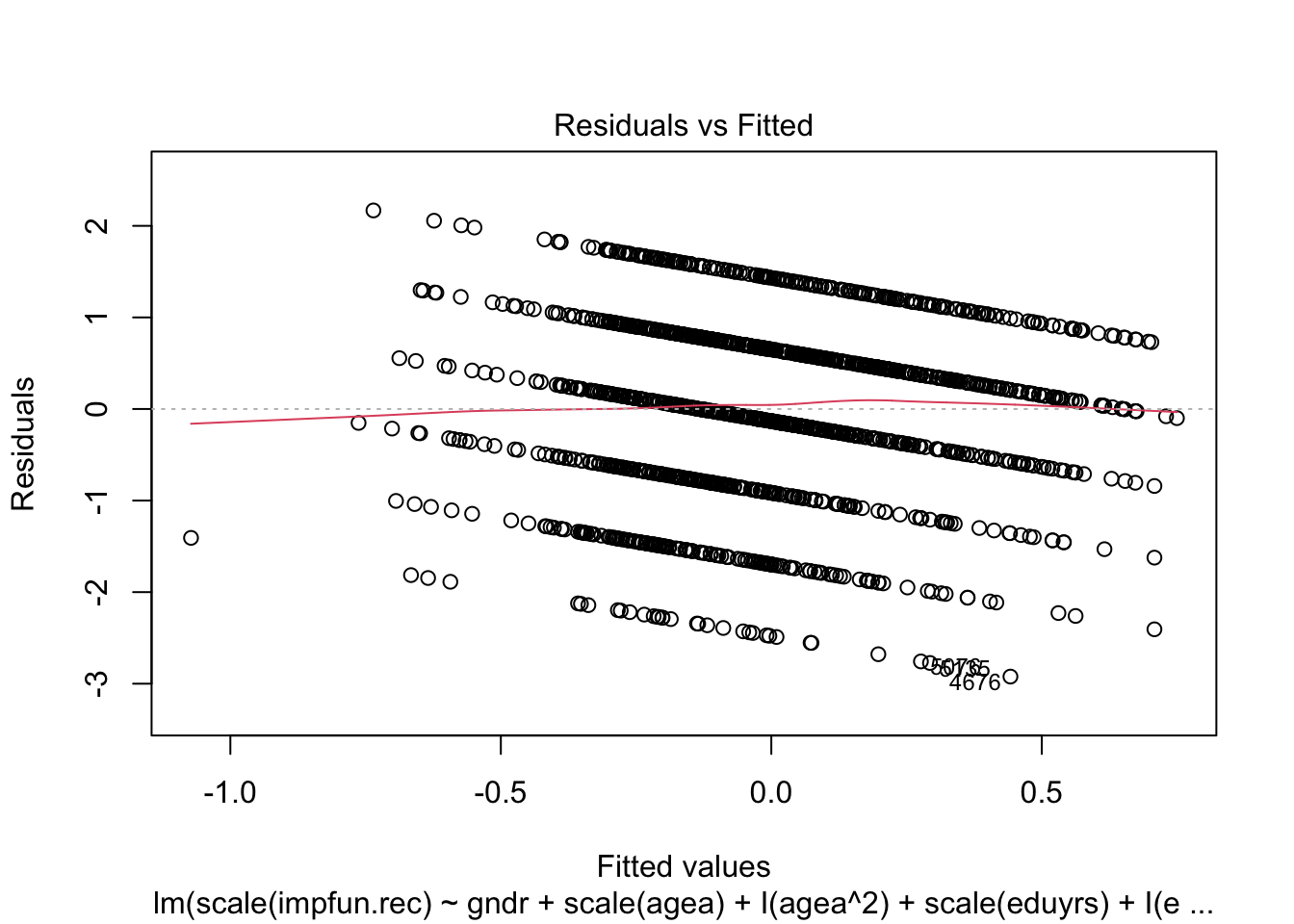
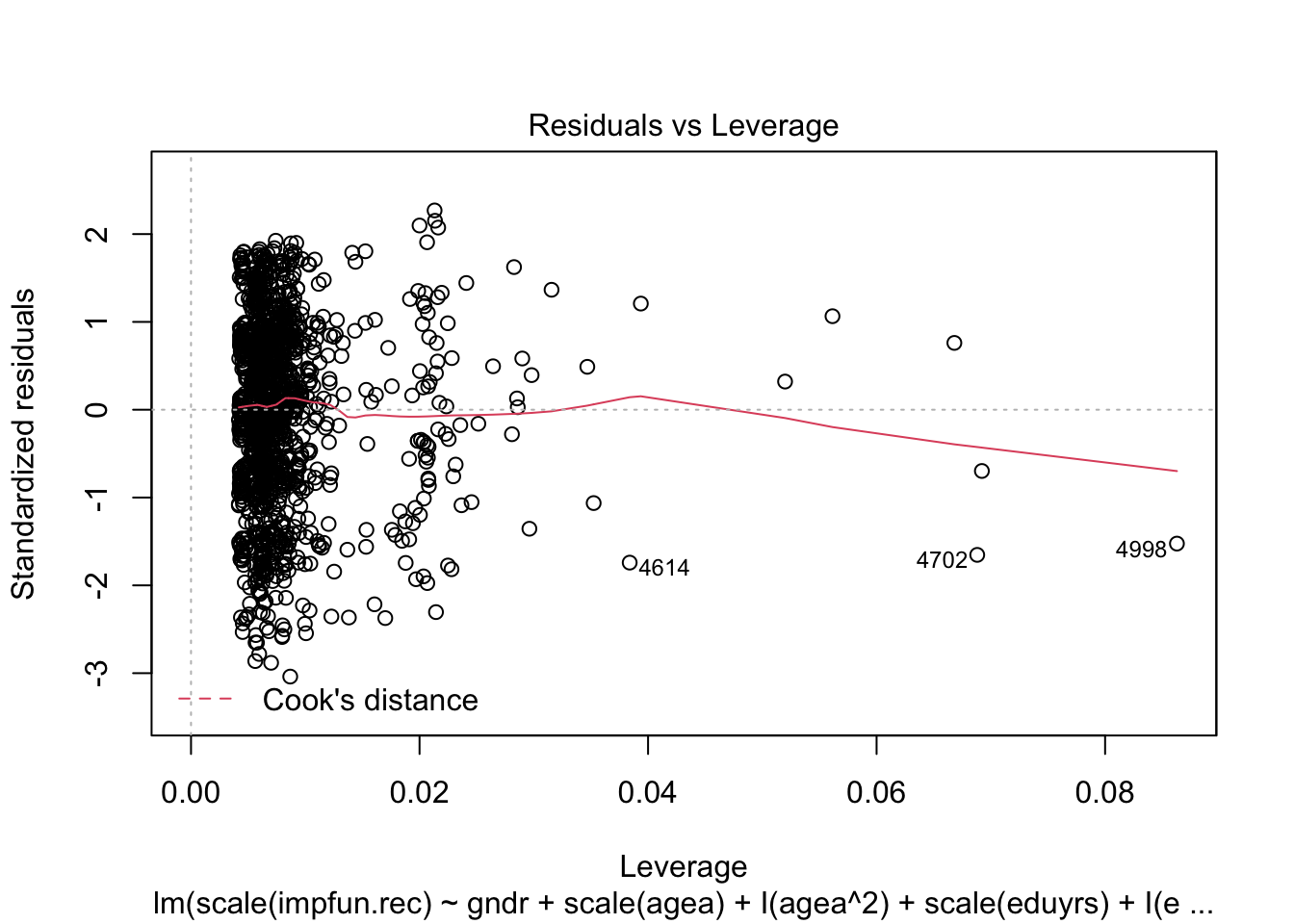
>                    GVIF Df GVIF^(1/(2*Df))
> gndr           1.006127  1        1.003059
> scale(agea)   27.258541  1        5.220971
> I(agea^2)     27.461828  1        5.240403
> scale(eduyrs) 30.336066  1        5.507819
> I(eduyrs^2)   30.277220  1        5.502474
> region         1.084653  6        1.006795

# на гетероскедастичность
lmtest::bptest(fit3)

> 
>   studentized Breusch-Pagan test
> 
> data:  fit3
> BP = 28.967, df = 11, p-value = 0.002297

car::ncvTest(fit3)

> Non-constant Variance Score Test 
> Variance formula: ~ fitted.values 
> Chisquare = 20.13085, Df = 1, p = 7.2321e-06

# Тест на нормальность распределения остатков
shapiro.test(residuals(fit3))

> 
>   Shapiro-Wilk normality test
> 
> data:  residuals(fit3)
> W = 0.98215, p-value = 9.889e-13

# ОПЦИОНАЛЬНО: зависимость остатков от предикторов - проверка на эндогенность - опциональная
summary(lm(residuals(fit3) ~ 
             fit3$model$gndr + 
             fit3$model$`scale(agea)` + fit3$model$`I(agea^2)` + 
             fit3$model$`scale(eduyrs)` + fit3$model$`I(eduyrs^2)` + 
             fit3$model$region))

> 
> Call:
> lm(formula = residuals(fit3) ~ fit3$model$gndr + fit3$model$`scale(agea)` + 
>     fit3$model$`I(agea^2)` + fit3$model$`scale(eduyrs)` + fit3$model$`I(eduyrs^2)` + 
>     fit3$model$region)
> 
> Residuals:
>      Min       1Q   Median       3Q      Max 
> -2.92234 -0.65386  0.07653  0.73301  2.16811 
> 
> Coefficients:
>                              Estimate Std. Error t value Pr(>|t|)
> (Intercept)                 7.277e-17  3.040e-01       0        1
> fit3$model$gndr             4.888e-17  4.993e-02       0        1
> fit3$model$`scale(agea)`    1.463e-16  1.301e-01       0        1
> fit3$model$`I(agea^2)`     -7.914e-20  7.029e-05       0        1
> fit3$model$`scale(eduyrs)` -1.864e-16  1.374e-01       0        1
> fit3$model$`I(eduyrs^2)`    1.208e-18  1.493e-03       0        1
> fit3$model$regionCH02       3.980e-17  7.886e-02       0        1
> fit3$model$regionCH03       2.188e-16  8.995e-02       0        1
> fit3$model$regionCH04       1.853e-16  8.734e-02       0        1
> fit3$model$regionCH05      -1.122e-16  8.909e-02       0        1
> fit3$model$regionCH06      -1.432e-17  9.871e-02       0        1
> fit3$model$regionCH07      -1.484e-16  1.435e-01       0        1
> 
> Residual standard error: 0.9659 on 1496 degrees of freedom
> Multiple R-squared:  4.473e-32,   Adjusted R-squared:  -0.007353 
> F-statistic: 6.083e-30 on 11 and 1496 DF,  p-value: 1

# ОПЦИОНАЛЬНО: корреляция между остатками и предсказанными значениями y - проверка на гетероскедастичность
cor(
  sqrt(abs(residuals(fit3))), 
  predict(fit3)
  )

> [1] -0.1348646

# ОПЦИОНАЛЬНО: Тест на нормальность зависимой переменной
shapiro.test(CH$impfun.rec)

> 
>   Shapiro-Wilk normality test
> 
> data:  CH$impfun.rec
> W = 0.91424, p-value < 2.2e-16

# ОПЦИОНАЛЬНО: Еше один тест на нормальность распределения остатков
ks.test(residuals(fit3), "pnorm", 0, sd(residuals(fit3))) # ties == repeated values

> 
>   One-sample Kolmogorov-Smirnov test
> 
> data:  residuals(fit3)
> D = 0.04793, p-value = 0.001959
> alternative hypothesis: two-sided

4 Задание 4 – интеракции

5 Взаимодействие предикторов – модерация

См. Пример в Лекции 3

http://apps.maksimrudnev.com/learn/paradox.Rmd

Добавьте в модель взаимодействие возраста и гендера. Постройте график интеракций и проитерпретируйте коэффициенты.

# Добавляем интеракцию между переменными используя символ звездочка * 
fit4 <- lm(scale(impfun.rec) ~ 
             gndr * scale(agea)  + I(agea^2) + 
             scale(eduyrs)  + I(eduyrs^2) +  
             region, 
           CH
           )

# смотрим на результаты
htab4 <- htmlreg(fit4)
browsable(HTML(htab4))

Statistical models
	Model 1
(Intercept)	0.10
	(0.30)
gndr	-0.10
	(0.05)
scale(agea)	-0.29^*
	(0.15)
agea^2	0.00^*
	(0.00)
scale(eduyrs)	0.05
	(0.14)
eduyrs^2	-0.00
	(0.00)
regionCH02	-0.27^***
	(0.08)
regionCH03	-0.27^**
	(0.09)
regionCH04	-0.36^***
	(0.09)
regionCH05	-0.10
	(0.09)
regionCH06	-0.23^*
	(0.10)
regionCH07	-0.61^***
	(0.14)
gndr:scale(agea)	-0.16^**
	(0.05)
R²	0.08
Adj. R²	0.07
Num. obs.	1508
^*p < 0.001; ^p < 0.01; ^*p < 0.05

# обязательно визуализируем для более точной интерпретации
plot_model(fit4, type = "eff", terms = c("agea", "gndr"))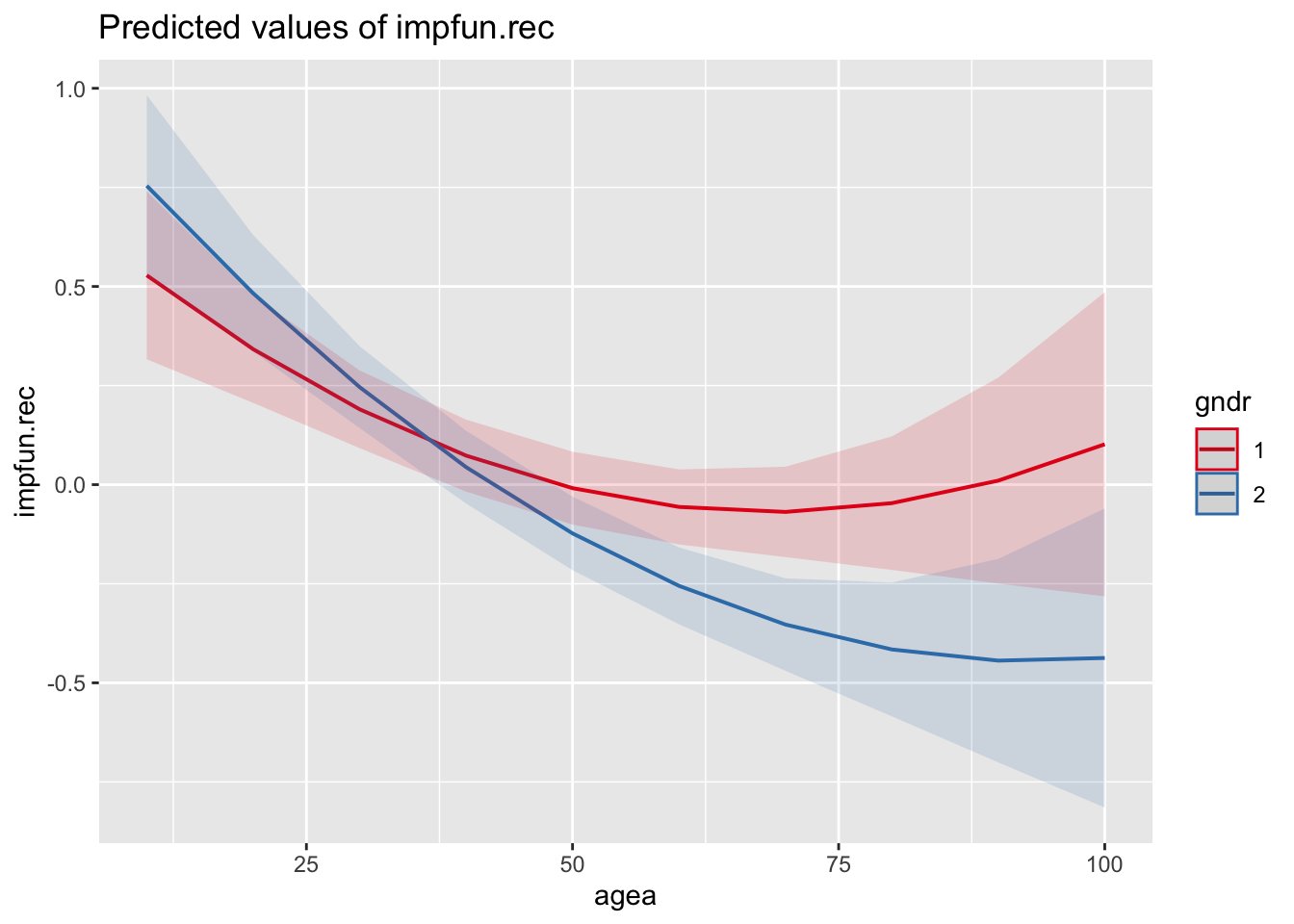

# сводим все модели в одну таблицу

htab.final <- htmlreg(list(fit1, fit2, fit3, fit4))
browsable(HTML(htab.final))

Statistical models
	Model 1	Model 2	Model 3	Model 4
(Intercept)	5.63^***	0.37^***	0.14	0.10
	(0.20)	(0.10)	(0.30)	(0.30)
gndr	-0.12	-0.10	-0.10	-0.10
	(0.06)	(0.05)	(0.05)	(0.05)
agea	-0.01^***
	(0.00)
eduyrs	-0.03^**
	(0.01)
regionCH02	-0.34^***	-0.27^***	-0.27^***	-0.27^***
	(0.10)	(0.08)	(0.08)	(0.08)
regionCH03	-0.34^**	-0.27^**	-0.27^**	-0.27^**
	(0.11)	(0.09)	(0.09)	(0.09)
regionCH04	-0.45^***	-0.35^***	-0.36^***	-0.36^***
	(0.11)	(0.09)	(0.09)	(0.09)
regionCH05	-0.13	-0.10	-0.10	-0.10
	(0.11)	(0.09)	(0.09)	(0.09)
regionCH06	-0.30^*	-0.24^*	-0.23^*	-0.23^*
	(0.13)	(0.10)	(0.10)	(0.10)
regionCH07	-0.78^***	-0.61^***	-0.62^***	-0.61^***
	(0.18)	(0.14)	(0.14)	(0.14)
scale(agea)		-0.21^***	-0.50^***	-0.29^*
		(0.03)	(0.13)	(0.15)
scale(eduyrs)		-0.07^**	0.07	0.05
		(0.03)	(0.14)	(0.14)
agea^2			0.00^*	0.00^*
			(0.00)	(0.00)
eduyrs^2			-0.00	-0.00
			(0.00)	(0.00)
gndr:scale(agea)				-0.16^**
				(0.05)
R²	0.07	0.07	0.07	0.08
Adj. R²	0.06	0.06	0.07	0.07
Num. obs.	1508	1508	1508	1508
^*p < 0.001; ^p < 0.01; ^*p < 0.05

6 👉🏻 Большое задание

Вычислите переменную – общее количество выпиваемого россиянами в неделю, используя две переменные:

alcwknd - количество выпитого алкоголя на выходных;
alcwkdy - количество выпитого алкоголя в рабочие дни.

Удалите из массива тех, кто не пил на этой неделе.

Попробуйте ответить на следующие вопросы:

Сколько всего в неделю выпивают российские мужчины и женщины (gndr)?
Коррелирует ли употребление алкоголя с возрастом (agea) и образованием (eduyrs)?
Влияют ли возраст, гендер, образование, наличие работы (icpdwrk) и партнера (icpart1), а также частота встреч с друзьями sclmeet и тип населенного пункта domicil на употребление алкоголя? Постройте регрессионные модели пошагово вводя каждую из независимых переменных. Меняются ли коэффициенты с добавлением предикторов? Почему?

# Считываем данные
library(foreign)

ess7 <- read.spss("data/Datafile_ESS7.sav", use.value.labels = F, to.data.frame=T)

# Отбираем россиян
ess7.RU <- ess7[ess7$cntry == "RU",]



# Делаем перекодировку для удобства
ess7.RU$gender <- factor(ess7.RU$gndr, labels = c("Male", "Female") )
ess7.RU$domicil <- factor(ess7.RU$domicil)

# Вычисляем зависимую переменную

ess7.RU$alcwkdy[ess7.RU$alcwkdy==5555] <- 0
ess7.RU$alcwknd[ess7.RU$alcwknd==5555] <- 0
ess7.RU$alc <- ess7.RU$alcwkdy + ess7.RU$alcwknd
ess7.RU$alc[ess7.RU$alc==0] <- NA

# Смотрим на распределение зависимой переменной
hist(ess7.RU$alc)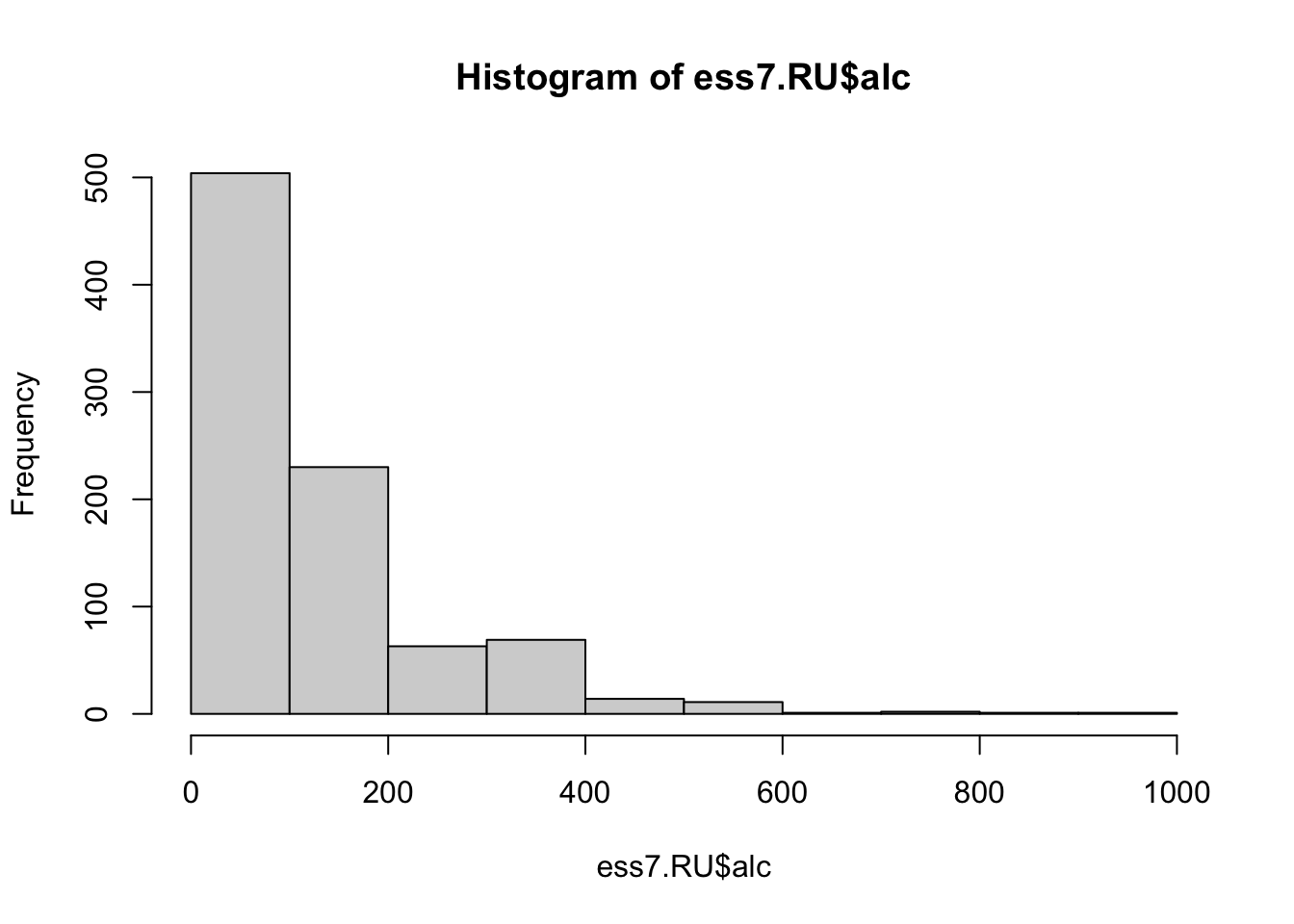

# Пошагово вводим предикторы
fit1 <- lm(alc ~ 
             agea , 
           data= ess7.RU
           )

fit2 <- lm(alc ~ 
             agea + gender , 
           data= ess7.RU
           )

fit3 <- lm(alc ~ 
             agea + gender + eduyrs, 
           data= ess7.RU
           )

fit4 <- lm(alc ~ 
             agea + gender + eduyrs + 
             sclmeet , 
           data= ess7.RU
           )

fit5 <- lm(alc ~ 
             agea + gender + eduyrs + 
             sclmeet + icpart1 + icpdwrk + domicil, 
           data= ess7.RU
           )

# Строим общую таблицу
regtab <- htmlreg(list(fit1, fit2, fit3, fit4, fit5))
browsable(HTML(regtab))

Statistical models
	Model 1	Model 2	Model 3	Model 4	Model 5
(Intercept)	101.26^***	125.18^***	180.34^***	182.46^***	162.80^***
	(12.66)	(12.62)	(25.87)	(29.51)	(34.45)
agea	0.77^**	0.92^***	0.78^**	0.77^**	0.88^**
	(0.27)	(0.27)	(0.27)	(0.28)	(0.29)
genderFemale		-63.46^***	-60.85^***	-59.76^***	-62.23^***
		(8.09)	(8.14)	(8.25)	(8.52)
eduyrs			-3.87^*	-4.15^**	-3.81^*
			(1.58)	(1.60)	(1.64)
sclmeet				0.27	-0.24
				(2.62)	(2.65)
icpart1					8.06
					(8.56)
icpdwrk					-4.89
					(9.68)
domicil2					69.99^**
					(24.54)
domicil3					17.13
					(9.49)
domicil4					3.72
					(10.84)
domicil5					5.86
					(60.55)
R²	0.01	0.07	0.08	0.08	0.09
Adj. R²	0.01	0.07	0.08	0.07	0.08
Num. obs.	896	896	896	883	883
^*p < 0.001; ^p < 0.01; ^*p < 0.05

Проверьте регрессионную модель на гетероскедастичность и мультиколлинеарность.

summary(fit5)

> 
> Call:
> lm(formula = alc ~ agea + gender + eduyrs + sclmeet + icpart1 + 
>     icpdwrk + domicil, data = ess7.RU)
> 
> Residuals:
>     Min      1Q  Median      3Q     Max 
> -198.47  -73.82  -33.06   37.87  737.50 
> 
> Coefficients:
>              Estimate Std. Error t value Pr(>|t|)    
> (Intercept)  162.8038    34.4523   4.725 2.68e-06 ***
> agea           0.8812     0.2933   3.005  0.00273 ** 
> genderFemale -62.2349     8.5215  -7.303 6.33e-13 ***
> eduyrs        -3.8147     1.6424  -2.323  0.02043 *  
> sclmeet       -0.2398     2.6504  -0.090  0.92794    
> icpart1        8.0582     8.5625   0.941  0.34692    
> icpdwrk       -4.8857     9.6805  -0.505  0.61390    
> domicil2      69.9915    24.5374   2.852  0.00444 ** 
> domicil3      17.1305     9.4897   1.805  0.07139 .  
> domicil4       3.7222    10.8393   0.343  0.73138    
> domicil5       5.8584    60.5542   0.097  0.92295    
> ---
> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> 
> Residual standard error: 120.1 on 872 degrees of freedom
>   (1562 observations deleted due to missingness)
> Multiple R-squared:  0.09041, Adjusted R-squared:  0.07998 
> F-statistic: 8.668 on 10 and 872 DF,  p-value: 1.288e-13

lmtest::bptest(fit5)

> 
>   studentized Breusch-Pagan test
> 
> data:  fit5
> BP = 33.089, df = 10, p-value = 0.0002631

car::ncvTest(fit5)

> Non-constant Variance Score Test 
> Variance formula: ~ fitted.values 
> Chisquare = 107.8896, Df = 1, p = < 2.22e-16

car::vif(fit5)

>             GVIF Df GVIF^(1/(2*Df))
> agea    1.217528  1        1.103416
> gender  1.109469  1        1.053314
> eduyrs  1.125247  1        1.060777
> sclmeet 1.072082  1        1.035414
> icpart1 1.119981  1        1.058291
> icpdwrk 1.207232  1        1.098741
> domicil 1.062740  4        1.007635

# plot(fit5)

Что влияет сильнее – возраст или образование? (Сравните стандартизованные коэффициенты).

# Стандартизируем интервальные переменные в модели
fit6 <- lm(scale(alc) ~ 
             scale(agea) + gender + scale(eduyrs) + 
             scale(sclmeet) + icpart1 + icpdwrk + domicil, 
           data= ess7.RU
           )

summary(fit6)

> 
> Call:
> lm(formula = scale(alc) ~ scale(agea) + gender + scale(eduyrs) + 
>     scale(sclmeet) + icpart1 + icpdwrk + domicil, data = ess7.RU)
> 
> Residuals:
>     Min      1Q  Median      3Q     Max 
> -1.5857 -0.5898 -0.2642  0.3026  5.8923 
> 
> Coefficients:
>                Estimate Std. Error t value Pr(>|t|)    
> (Intercept)     0.15450    0.14166   1.091  0.27573    
> scale(agea)     0.12539    0.04173   3.005  0.00273 ** 
> genderFemale   -0.49723    0.06808  -7.303 6.33e-13 ***
> scale(eduyrs)  -0.08686    0.03740  -2.323  0.02043 *  
> scale(sclmeet) -0.00318    0.03515  -0.090  0.92794    
> icpart1         0.06438    0.06841   0.941  0.34692    
> icpdwrk        -0.03904    0.07734  -0.505  0.61390    
> domicil2        0.55921    0.19604   2.852  0.00444 ** 
> domicil3        0.13687    0.07582   1.805  0.07139 .  
> domicil4        0.02974    0.08660   0.343  0.73138    
> domicil5        0.04681    0.48380   0.097  0.92295    
> ---
> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> 
> Residual standard error: 0.9597 on 872 degrees of freedom
>   (1562 observations deleted due to missingness)
> Multiple R-squared:  0.09041, Adjusted R-squared:  0.07998 
> F-statistic: 8.668 on 10 and 872 DF,  p-value: 1.288e-13

Введите интеракцию (взаимодействие) между гендером и возрастом и попробуйте проинтерпретировать результаты.

# Добавляем интеракцию
fit7 <- lm(scale(alc) ~ 
             scale(agea) * gender + scale(eduyrs) + 
             scale(sclmeet) + icpart1 + icpdwrk + domicil, 
           data= ess7.RU
           )

# Смотрим на результаты
summary(fit7)

> 
> Call:
> lm(formula = scale(alc) ~ scale(agea) * gender + scale(eduyrs) + 
>     scale(sclmeet) + icpart1 + icpdwrk + domicil, data = ess7.RU)
> 
> Residuals:
>     Min      1Q  Median      3Q     Max 
> -1.9238 -0.5596 -0.2517  0.2858  6.0092 
> 
> Coefficients:
>                           Estimate Std. Error t value Pr(>|t|)    
> (Intercept)               0.152166   0.139948   1.087  0.27720    
> scale(agea)               0.292984   0.054334   5.392 8.96e-08 ***
> genderFemale             -0.554140   0.068327  -8.110 1.71e-15 ***
> scale(eduyrs)            -0.094178   0.036978  -2.547  0.01104 *  
> scale(sclmeet)           -0.007048   0.034738  -0.203  0.83926    
> icpart1                   0.106477   0.068168   1.562  0.11866    
> icpdwrk                  -0.049712   0.076444  -0.650  0.51566    
> domicil2                  0.513659   0.193918   2.649  0.00822 ** 
> domicil3                  0.115680   0.075038   1.542  0.12353    
> domicil4                  0.028053   0.085558   0.328  0.74308    
> domicil5                  0.154685   0.478511   0.323  0.74657    
> scale(agea):genderFemale -0.360537   0.076133  -4.736 2.55e-06 ***
> ---
> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> 
> Residual standard error: 0.9481 on 871 degrees of freedom
>   (1562 observations deleted due to missingness)
> Multiple R-squared:  0.1132,  Adjusted R-squared:  0.102 
> F-statistic: 10.11 on 11 and 871 DF,  p-value: < 2.2e-16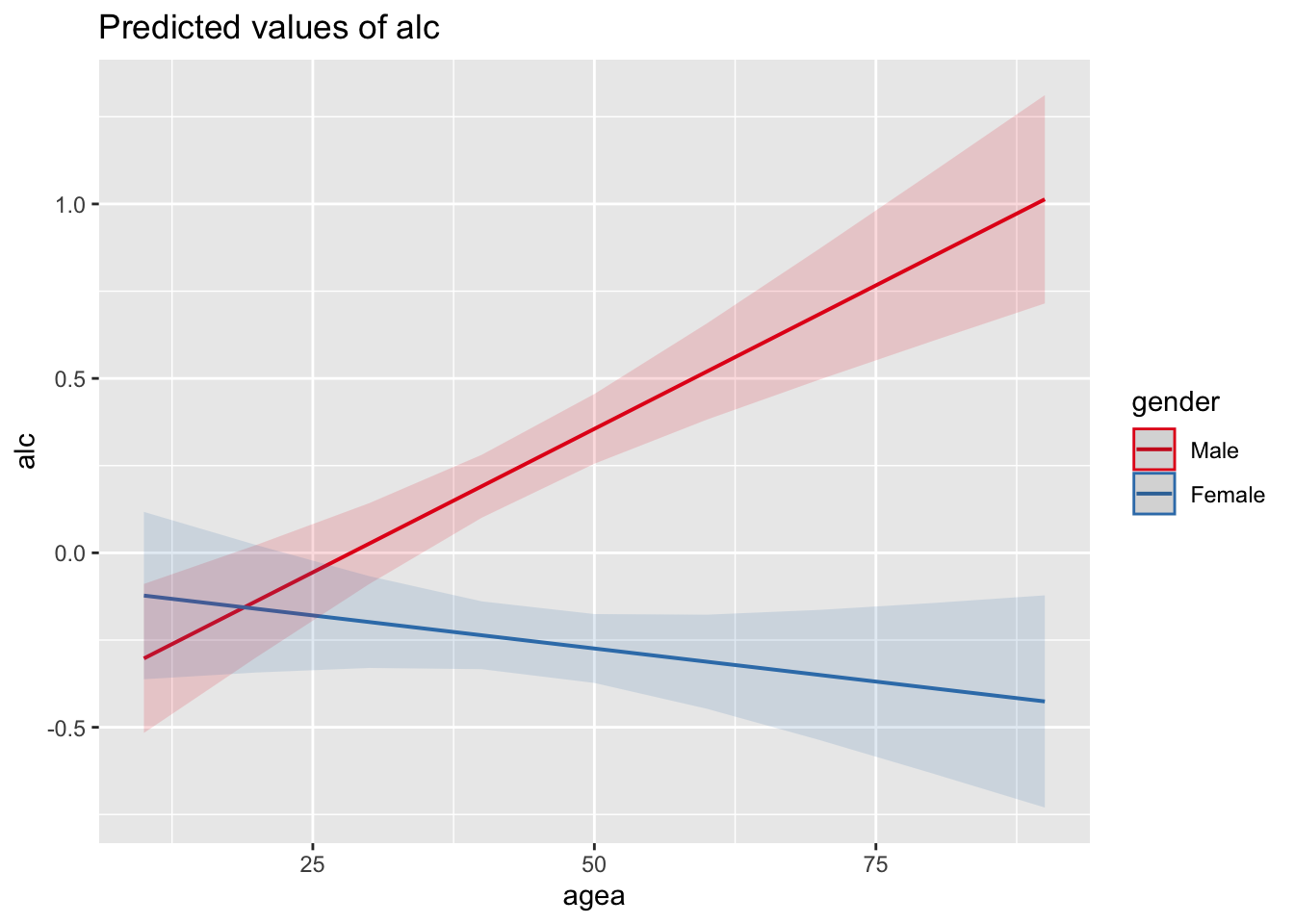

# Строим график
plot_model(fit7, type = "eff", terms = c("agea", "gender"))

Добавьте в модель квадратичный эффект возраста и посмотрите на то, как изменились результаты.

# Добавили квадрат возраста 
fit8 <- lm(scale(alc) ~ 
             scale(agea) * gender + scale(eduyrs) + I(agea^2) +
             scale(sclmeet) + icpart1 + icpdwrk + domicil, 
           data= ess7.RU
           )

# Смотрим результаты
summary(fit8)

> 
> Call:
> lm(formula = scale(alc) ~ scale(agea) * gender + scale(eduyrs) + 
>     I(agea^2) + scale(sclmeet) + icpart1 + icpdwrk + domicil, 
>     data = ess7.RU)
> 
> Residuals:
>     Min      1Q  Median      3Q     Max 
> -1.6677 -0.5746 -0.2401  0.2911  6.0143 
> 
> Coefficients:
>                            Estimate Std. Error t value Pr(>|t|)    
> (Intercept)               1.5409153  0.3333232   4.623 4.36e-06 ***
> scale(agea)               1.3850904  0.2444472   5.666 1.98e-08 ***
> genderFemale             -0.5970626  0.0682043  -8.754  < 2e-16 ***
> scale(eduyrs)            -0.1157746  0.0368642  -3.141  0.00174 ** 
> I(agea^2)                -0.0006891  0.0001505  -4.580 5.34e-06 ***
> scale(sclmeet)            0.0078545  0.0345005   0.228  0.81996    
> icpart1                   0.1679374  0.0687230   2.444  0.01474 *  
> icpdwrk                   0.0902557  0.0815278   1.107  0.26858    
> domicil2                  0.4782636  0.1918879   2.492  0.01287 *  
> domicil3                  0.1213557  0.0742023   1.635  0.10231    
> domicil4                  0.0048130  0.0847454   0.057  0.95472    
> domicil5                  0.0675881  0.4734994   0.143  0.88653    
> scale(agea):genderFemale -0.3309026  0.0755521  -4.380 1.33e-05 ***
> ---
> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> 
> Residual standard error: 0.9374 on 870 degrees of freedom
>   (1562 observations deleted due to missingness)
> Multiple R-squared:  0.1341,  Adjusted R-squared:  0.1222 
> F-statistic: 11.23 on 12 and 870 DF,  p-value: < 2.2e-16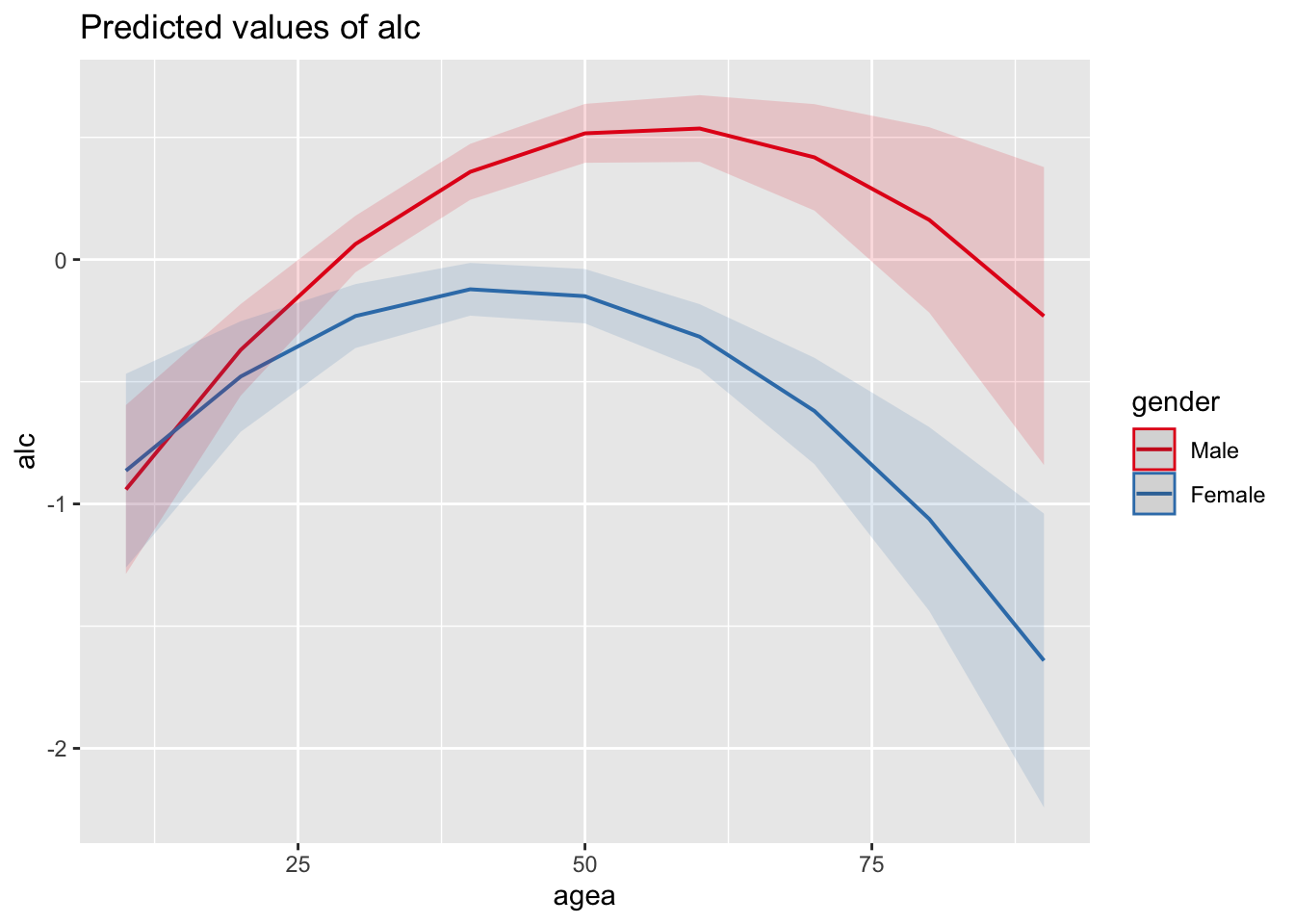

# Визуализируем связь
plot_model(fit8, type = "eff", terms = c("agea", "gender"))

Сравните полученные модели между собой: стабильность коэффициентов и стандартных ошибок, качество объяснения и нарушение допущений.

# Сводим результаты последних трех моделей  в едтиную таблицу
regtab <- htmlreg(list(fit6, fit7, fit8))
browsable(HTML(regtab))

Statistical models
	Model 1	Model 2	Model 3
(Intercept)	0.15	0.15	1.54^***
	(0.14)	(0.14)	(0.33)
scale(agea)	0.13^**	0.29^***	1.39^***
	(0.04)	(0.05)	(0.24)
genderFemale	-0.50^***	-0.55^***	-0.60^***
	(0.07)	(0.07)	(0.07)
scale(eduyrs)	-0.09^*	-0.09^*	-0.12^**
	(0.04)	(0.04)	(0.04)
scale(sclmeet)	-0.00	-0.01	0.01
	(0.04)	(0.03)	(0.03)
icpart1	0.06	0.11	0.17^*
	(0.07)	(0.07)	(0.07)
icpdwrk	-0.04	-0.05	0.09
	(0.08)	(0.08)	(0.08)
domicil2	0.56^**	0.51^**	0.48^*
	(0.20)	(0.19)	(0.19)
domicil3	0.14	0.12	0.12
	(0.08)	(0.08)	(0.07)
domicil4	0.03	0.03	0.00
	(0.09)	(0.09)	(0.08)
domicil5	0.05	0.15	0.07
	(0.48)	(0.48)	(0.47)
scale(agea):genderFemale		-0.36^***	-0.33^***
		(0.08)	(0.08)
agea^2			-0.00^***
			(0.00)
R²	0.09	0.11	0.13
Adj. R²	0.08	0.10	0.12
Num. obs.	883	883	883
^*p < 0.001; ^p < 0.01; ^*p < 0.05

Данные: Datafile_ESS7.sav

По итогам попробуйте составить целиковый работающий скрипт. Очистите память, перезапустите сессию R и запустите весь скрипт целиком. Если скрипт не запускается, найдите в нем ошибки и доведите код до безошибочного вида.

Максим Руднев, 2018-2021 на основе RMarkdown.

Регрессии

сентябрь 2021г.