1 🔦 Разведывательный (эксплораторный) факторный анализ

  • Для чего нужен разведывательный ФА?

  • В какой ситуации РФА может понадобиться?

  • Что является результатом РФА?

  • Как определять количество факторов в РФА?

  • Как интерпретировать факторные нагрузки?

  • Необходимо ли вращение факторов?

  • Как осуществляется вращение?

  • Какие методы вращения существуют?

1.1 Задача

Мы изучаем ценности португальцев.

У нас есть 9 индикаторов ценностей: важность для респондента

  • свободы (free),
  • креативности (creative),
  • постоянных приключений (adventures),
  • пробы нового, разного (different),
  • хорошего времяпрепровождения (good.time),
  • веселья (fun),
  • следования правилам (follow.rules),
  • скромности (modest)
  • безопасности (safety).

Латентные переменные, которые мы ищем – жизненные ценности человека, (отрицательно и/или положительно) связанные с открытостью. Однако, мы пока не представляем сколько этих латентных переменных и каким образом они друг с другом связаны. Поэтому начнем построение измерительной модели с разведывательного факторного анализа (функция factanal()).

Данные

Скачайте готовый объект с данными - PT.values.R и считайте его функцией load().

1.2 Критерий сферичности Бартлетта

Отвечает на вопрос:

Есть ли хоть одна существенная корреляция между нашими переменными?

Очень слабый тест, т.к. нулевая гипотеза очень маловероятна в практической ситуации.

# создаем матрицу корреляций
PT.cor <- cor(PT.values, use = "complete")

# смотрим на матрицу корреляций
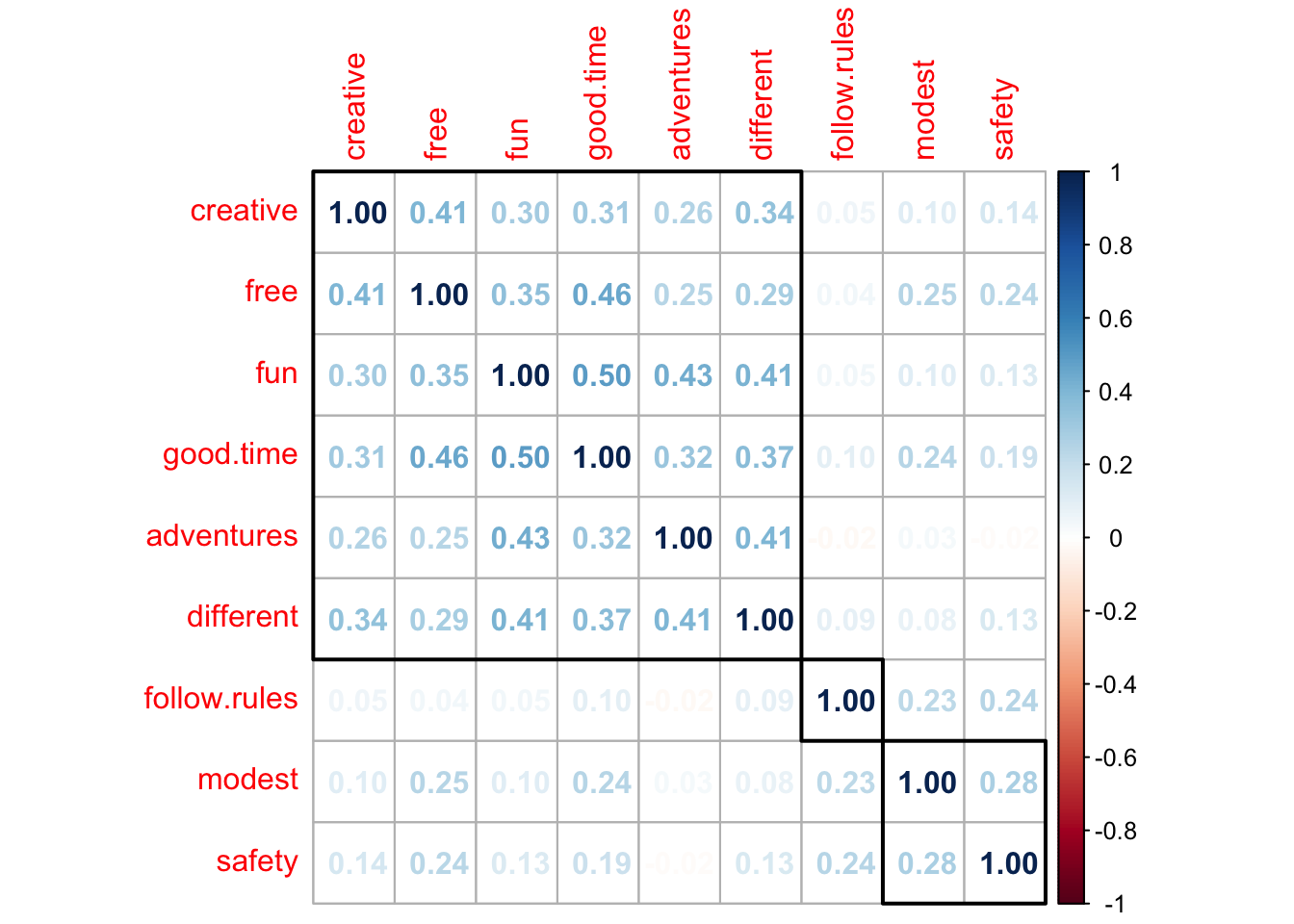
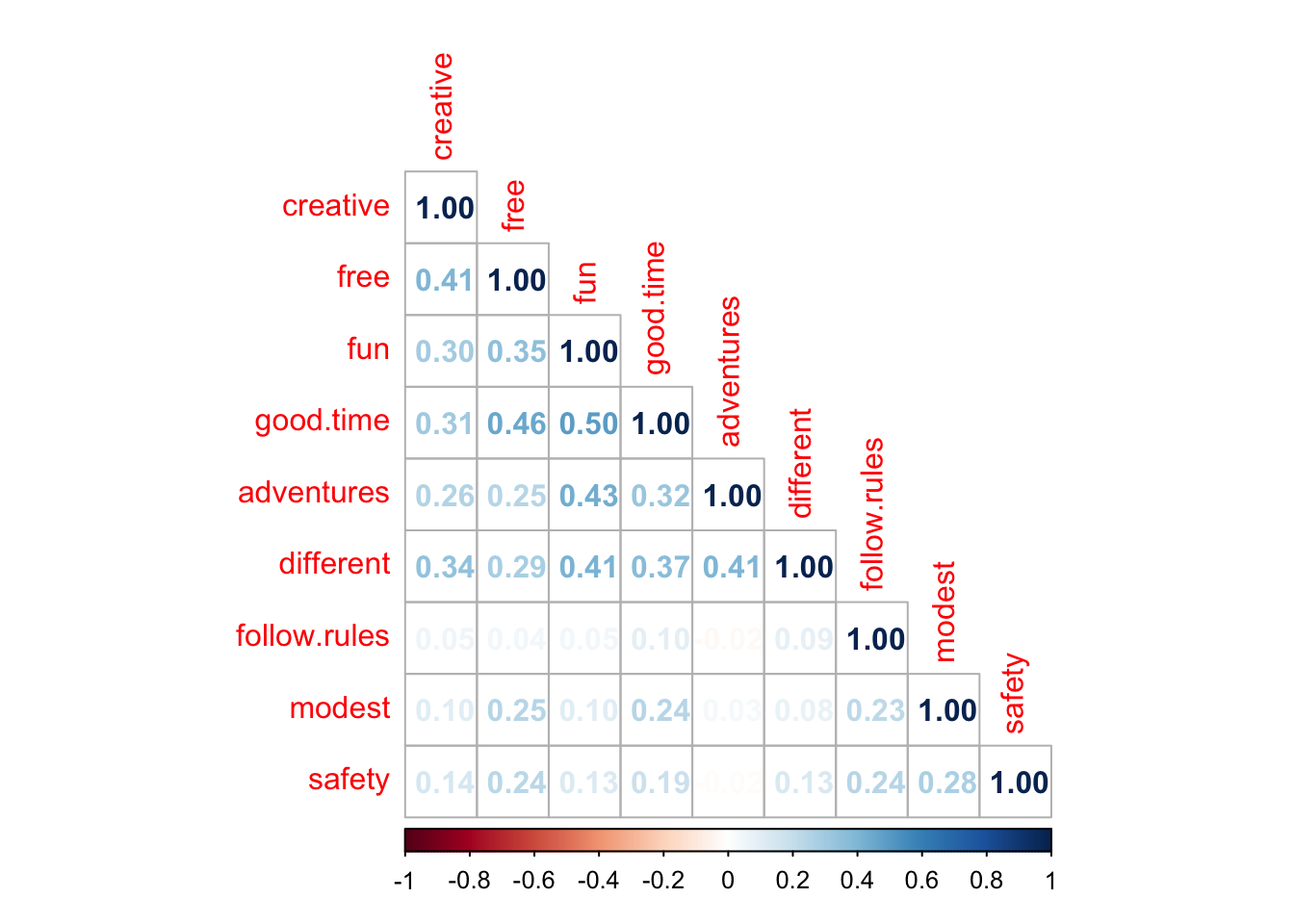
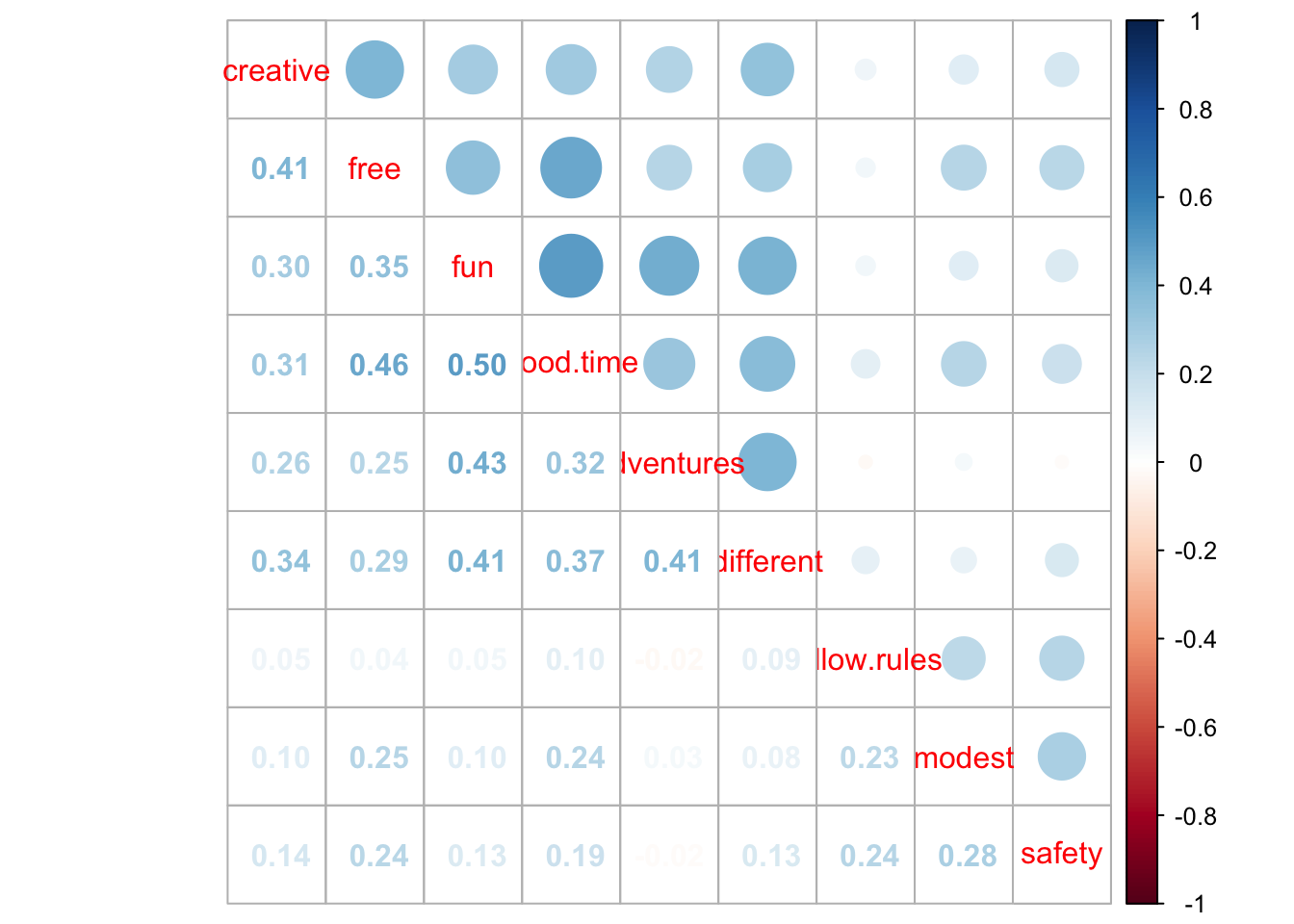
round(PT.cor, 2)
>              creative free  fun adventures different good.time follow.rules modest safety
> creative         1.00 0.41 0.30       0.26      0.34      0.31         0.05   0.10   0.14
> free             0.41 1.00 0.35       0.25      0.29      0.46         0.04   0.25   0.24
> fun              0.30 0.35 1.00       0.43      0.41      0.50         0.05   0.10   0.13
> adventures       0.26 0.25 0.43       1.00      0.41      0.32        -0.02   0.03  -0.02
> different        0.34 0.29 0.41       0.41      1.00      0.37         0.09   0.08   0.13
> good.time        0.31 0.46 0.50       0.32      0.37      1.00         0.10   0.24   0.19
> follow.rules     0.05 0.04 0.05      -0.02      0.09      0.10         1.00   0.23   0.24
> modest           0.10 0.25 0.10       0.03      0.08      0.24         0.23   1.00   0.28
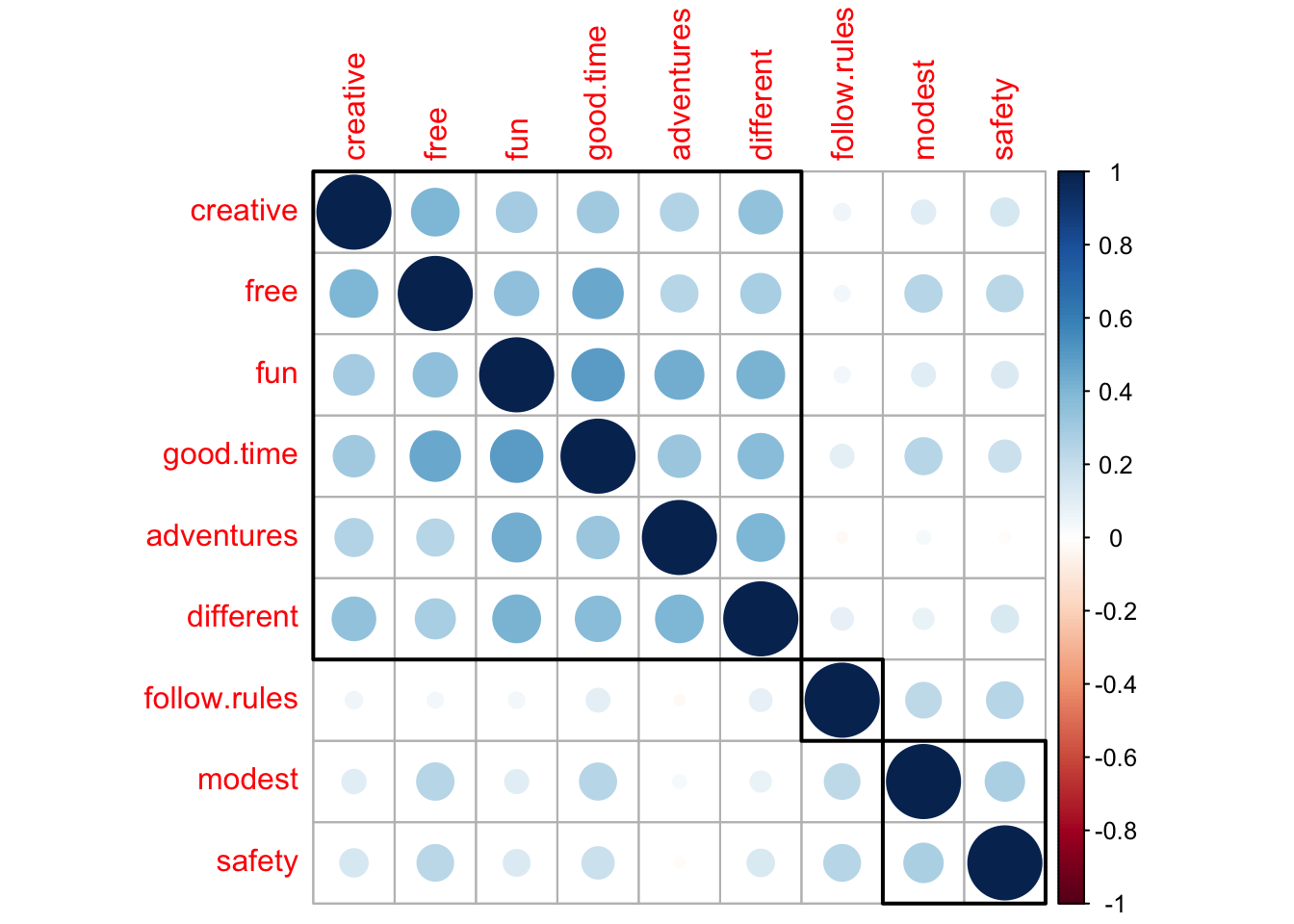
> safety           0.14 0.24 0.13      -0.02      0.13      0.19         0.24   0.28   1.00

🔵 Корреляционные графики

library("corrplot")

circle
corrplot(PT.cor, 
         method = "circle",
         order = "hclust",
         addrect = 3
         )

number
corrplot(PT.cor, 
         method = "number",
         order = "hclust",
         addrect = 3
         )

pie
corrplot(PT.cor, 
         method = "pie",
         order = "hclust",
         addrect = 3
         )

lower
corrplot(PT.cor, 
         method = "number",
         order = "hclust",
         addrect = 3,
         type = "lower"
         )

mixed
corrplot.mixed(PT.cor, 
               lower = "number",
               upper = "circle",
               order = "hclust"  
         )

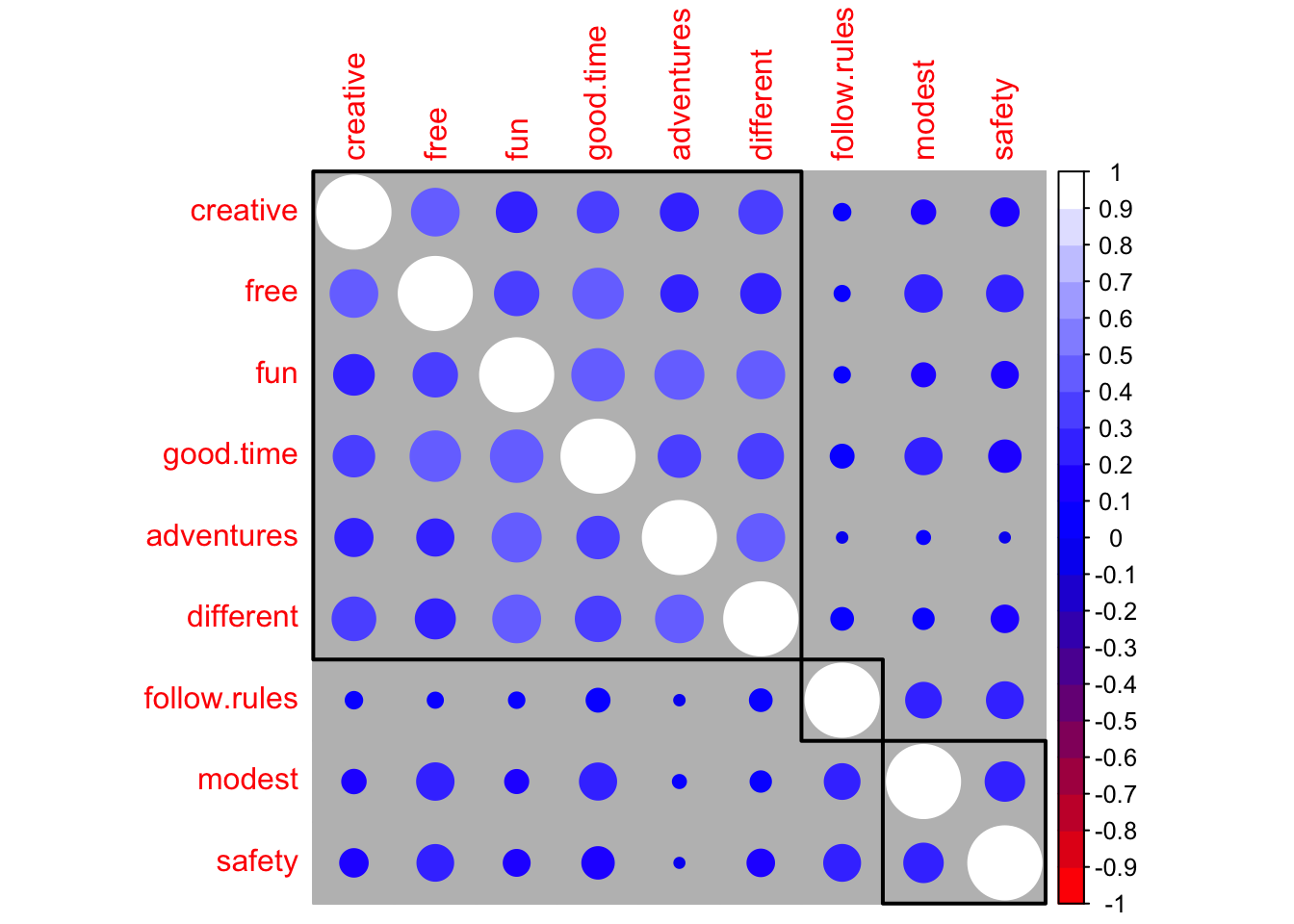
colors
corrplot(PT.cor, 
             method = "circle",  
             order = "hclust",
             addrect = 3,
             col = colorRampPalette( c("red", "blue", "white"))(20),
             bg = "gray"
         )  

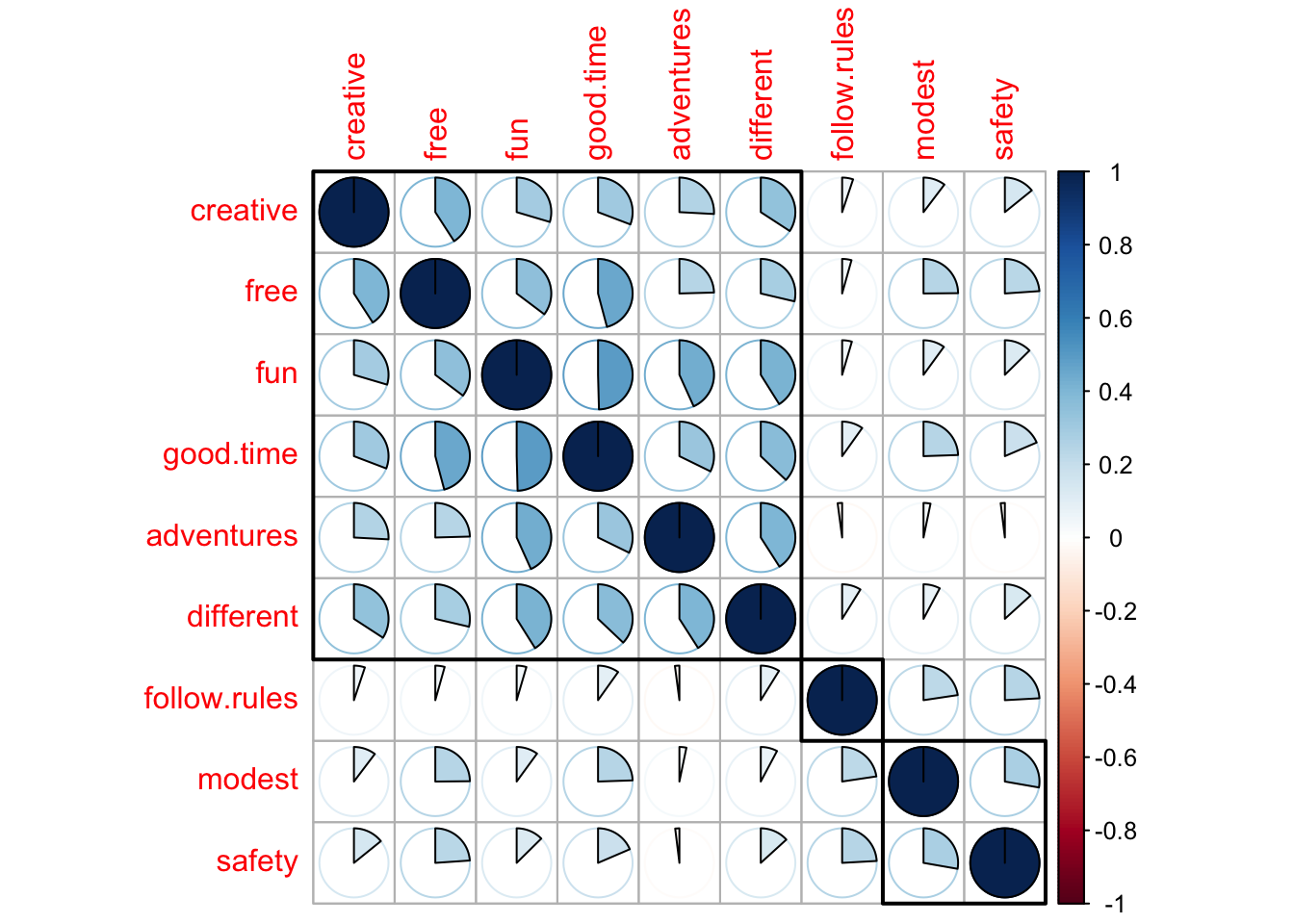
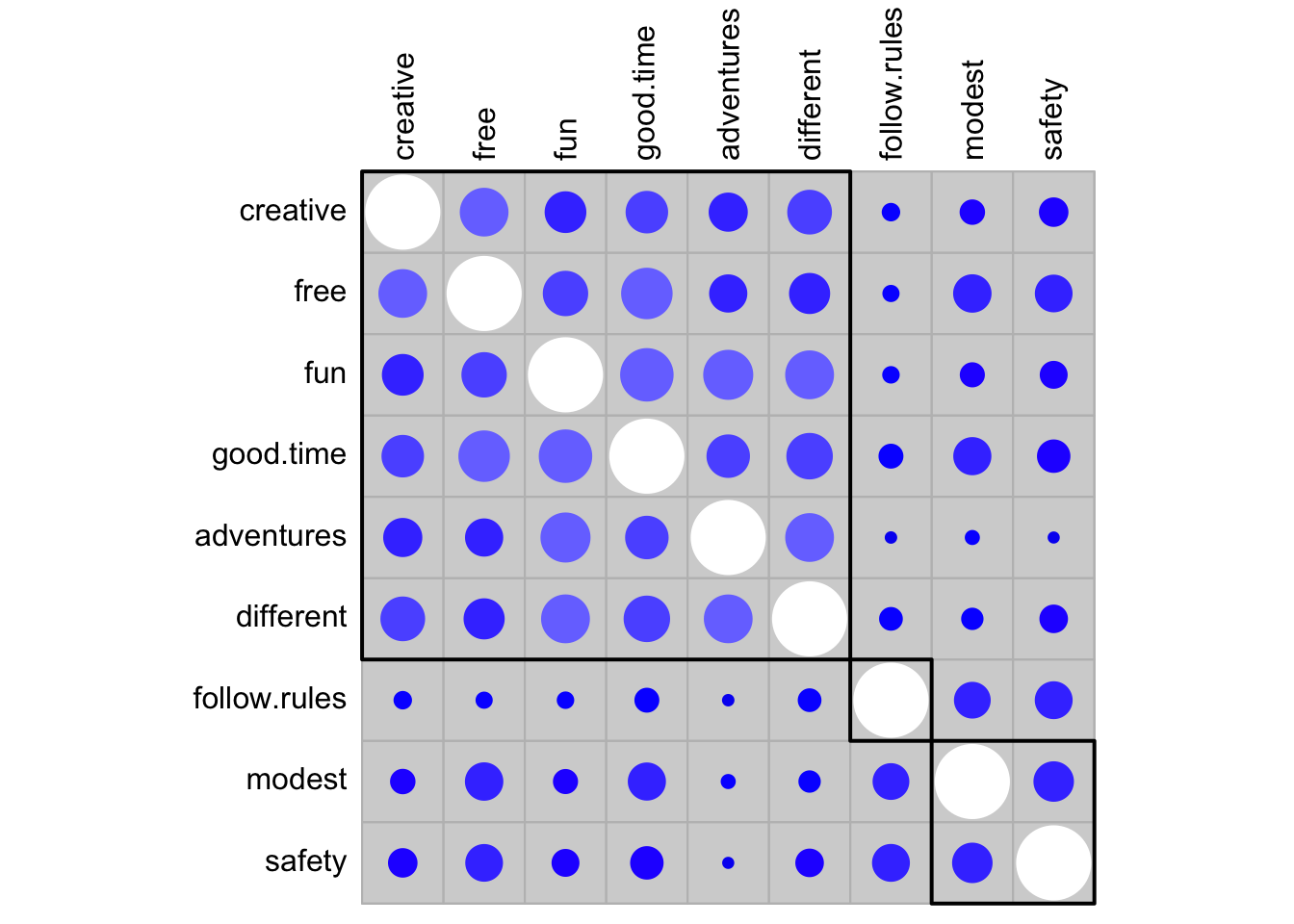
corrplot( PT.cor,
          method="circle",  
          order="hclust",
          addrect=3,
          col=colorRampPalette( c("red", "blue", "white"))(20),
          bg="light gray",
          cl.pos = "n",      # убираем цветовую легенду
          tl.col="black"     # меняем цвет текстовых подписей
         )  

# Собственно тест Бартлетта
library("psych")

cortest.bartlett(PT.cor, n = nrow(na.omit(PT.values)))
> $chisq
> [1] 2019.395
> 
> $p.value
> [1] 0
> 
> $df
> [1] 36

Тест предсказуемо высоко значим, значит не все корреляции между нашими переменными равны нулю.

1.3 Определение количества факторов

library('nFactors')

PT.scree <- nScree(PT.cor, model = "factors")

plot(PT.scree)

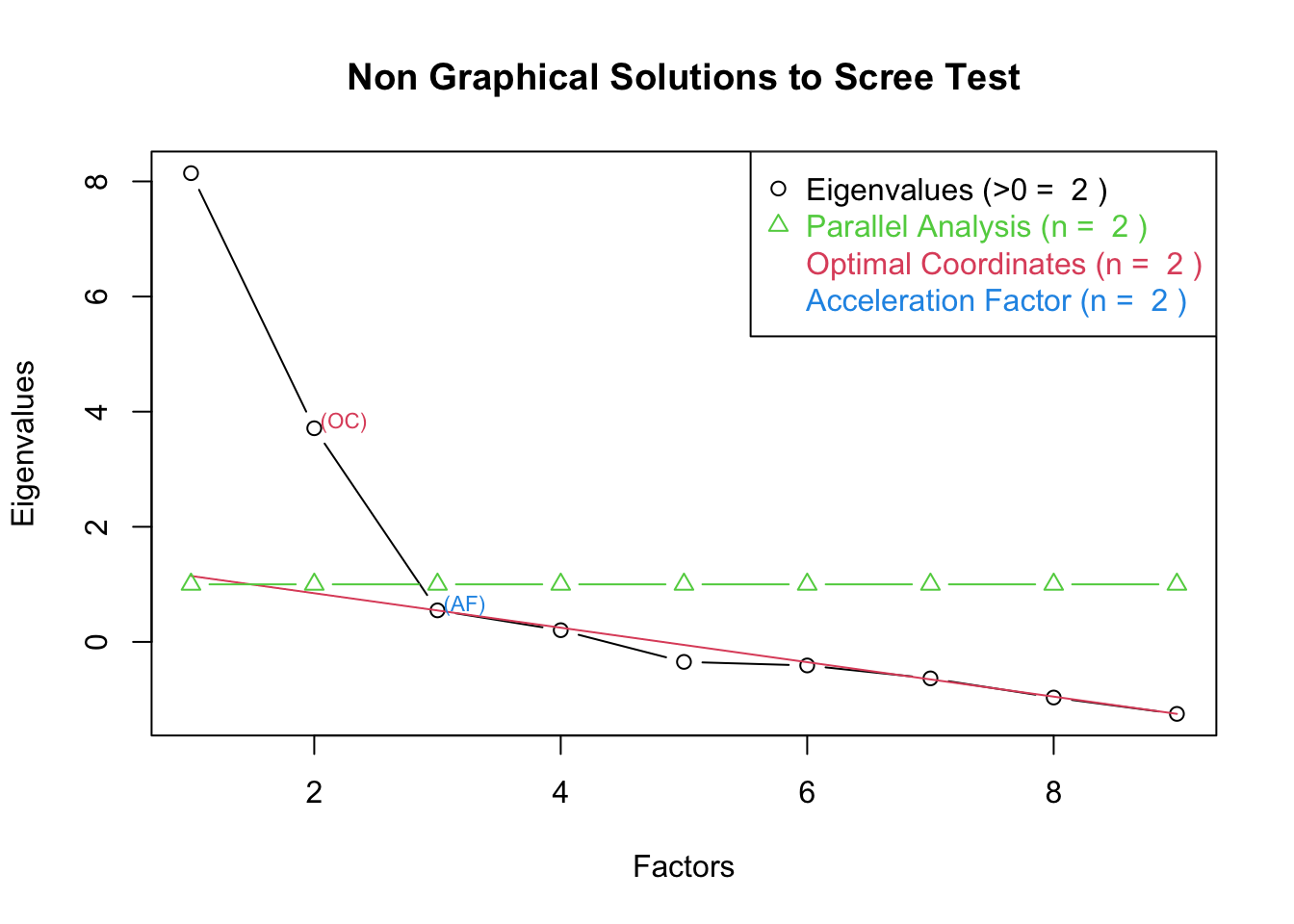
Eigenvalues = собственные значения, репрезентирующие дисперсию, объясненную каждым фактором. Единица соответствует дисперсии, равной средней дисперсии одной переменной из нашего набора.

Каменистая осыпь (scree test) - определить место перелома линии визуально.

Правило Кайзера - количество факторов равно количеству собственных значений больше 1.

Optimal coordinates – Оптимальные координаты – между каждой парой (k и k + 1) точек на графике считается регрессия и если она предсказывает третью точку (k + 2), то количество факторов считается достаточным и равным k + 1.

Acceleration factor – Коэффициент акселерации – определение количества факторов на основе второй производной. Указывает на место изгиба кривой – “локтя”.

👎🏻 Параллельный анализ – генерирует случайные данные

для них вычисляются собственные значения и затем сравниваются с собственными значениями, полученными на реальных данных. По сути, пытается отделить факторы, потенциально сгенерированные “шумом” от тех, которые “шумом” точно не являются . См. подробнее.

Хи-квадрат – та же интерпретация, что и в структурных моделях. Можно увеличивать количество факторов до тех пор, пока хи-квадрат не станет незначимым (например, p-значение больше 0,05). Доступен в случае, если для поиска факторов использовался метод наибольшего правдоподобия (ML – maximum likelihood).

В данном случае критерии предлагают 2 фактора, хотя можно рассмотреть и 3-хфакторное решение.

1.4 Построение факторов

EFA1 <- factanal(
                 na.omit(PT.values),
                 factors = 1
                 )
EFA1
> 
> Call:
> factanal(x = na.omit(PT.values), factors = 1)
> 
> Uniquenesses:
>     creative         free          fun   adventures    different    good.time follow.rules       modest 
>        0.739        0.636        0.552        0.733        0.661        0.514        0.985        0.931 
>       safety 
>        0.934 
> 
> Loadings:
>              Factor1
> creative     0.511  
> free         0.603  
> fun          0.669  
> adventures   0.517  
> different    0.582  
> good.time    0.697  
> follow.rules 0.124  
> modest       0.262  
> safety       0.258  
> 
>                Factor1
> SS loadings      2.316
> Proportion Var   0.257
> 
> Test of the hypothesis that 1 factor is sufficient.
> The chi square statistic is 406.63 on 27 degrees of freedom.
> The p-value is 2.23e-69

В данном коде мы запрашиваем один фактор c девятью индикаторами, полностью исключая пропущенные данные. Вращение в случае одного фактора не имеет смысла, также как и для поиска количества факторов – как факторы не вращай, статистики согласия останутся теми же.

Далее мы будем использовать косоугольное Geomin вращение, так как оно хорошо соответствует дальнейшему КФА и у нас нет ожиданий насчет того, что латентные переменные не скоррелированы.

Повторите эту процедуру для двух- и трехфакторного решения и посмотрите на статистику согласия хи-квадрат.

которые по отдельности можно запросить так:

EFA1$STATISTIC  # значение хи-квадрата модели EFA1
EFA1$dof        # количество степеней свободы модели EFA1
EFA1$PVAL       # значимость хи-квадрата модели EFA1
round(EFA1$PVAL, 4)
> objective 
>         0

1.5 Сравнение факторных моделей

Модели с разным количеством факторов являются вложенными, значит их можно сравнивать хи-квадратом. Сделаем это вручную, написав код, сохраняющий разницу между хи-квадратами и между степенями свободы моделей с 2-мя и 3-мя факторами в объекты chisq.difference и df.difference, а затем найдем значимость получившейся разницы с помощью следующей команды, отображающей p-значения из распределения хи-квадрат.

# эта строка возвращает p-значение хи-квадрата с заданными степенями свободы
1-pchisq(chisq.difference, df.difference)
EFA2 <- factanal(
                 na.omit(PT.values),
                 factors = 2
                 )

EFA3 <- factanal(
                 na.omit(PT.values),
                 factors = 3
                 )

chisq.difference <- EFA2$STATISTIC - EFA3$STATISTIC
df.difference <- EFA2$dof - EFA3$dof
1-pchisq(chisq.difference, df.difference)
>    objective 
> 1.654232e-14

Не обращайте внимание на слово objective, выведенная информация – это p-значение разницы хи-квадратов.

Из этих статистик следует, что из двух рассмотренных лучше к данным подходит модель с ___ факторами.

1.6 Рассмотрение нагрузок

Для того, чтобы узнать, какие индикаторы приписывать какому фактору, а какие из них фиксировать равными нулю, рассмотрим факторные нагрузки из РФА и подумаем исходя из теоретической значимости получаемых латентных переменных.

library("GPArotation")

EFA2 <- factanal(
                na.omit(PT.values),
                factors = 2, 
                rotation = "geominQ"
                )

print(
      EFA2, 
      digits = 2, # до какого знака округлять
      cutoff = 0, # не выводить факторные нагрузки ниже этого значения
      sort = TRUE # сортировать ли нагрузки по первому фактору?
      )
> 
> Call:
> factanal(x = na.omit(PT.values), factors = 2, rotation = "geominQ")
> 
> Uniquenesses:
>     creative         free          fun   adventures    different    good.time follow.rules       modest 
>         0.74         0.61         0.52         0.59         0.63         0.52         0.87         0.71 
>       safety 
>         0.71 
> 
> Loadings:
>              Factor1 Factor2
> fun           0.70   -0.01  
> adventures    0.66   -0.22  
> different     0.61   -0.01  
> good.time     0.59    0.23  
> modest        0.02    0.53  
> safety        0.02    0.53  
> creative      0.46    0.12  
> free          0.46    0.31  
> follow.rules -0.05    0.37  
> 
>                Factor1 Factor2
> SS loadings       2.08    0.91
> Proportion Var    0.23    0.10
> Cumulative Var    0.23    0.33
> 
> Factor Correlations:
>         Factor1 Factor2
> Factor1    1.00   -0.28
> Factor2   -0.28    1.00
> 
> Test of the hypothesis that 2 factors are sufficient.
> The chi square statistic is 134.08 on 19 degrees of freedom.
> The p-value is 2.45e-19
# View(as.data.frame.matrix(loadings(EFA2)))

Или на графиках

dat.for.plot <- as.data.frame.matrix(loadings(EFA2))

plot(dat.for.plot); text(dat.for.plot, rownames(dat.for.plot))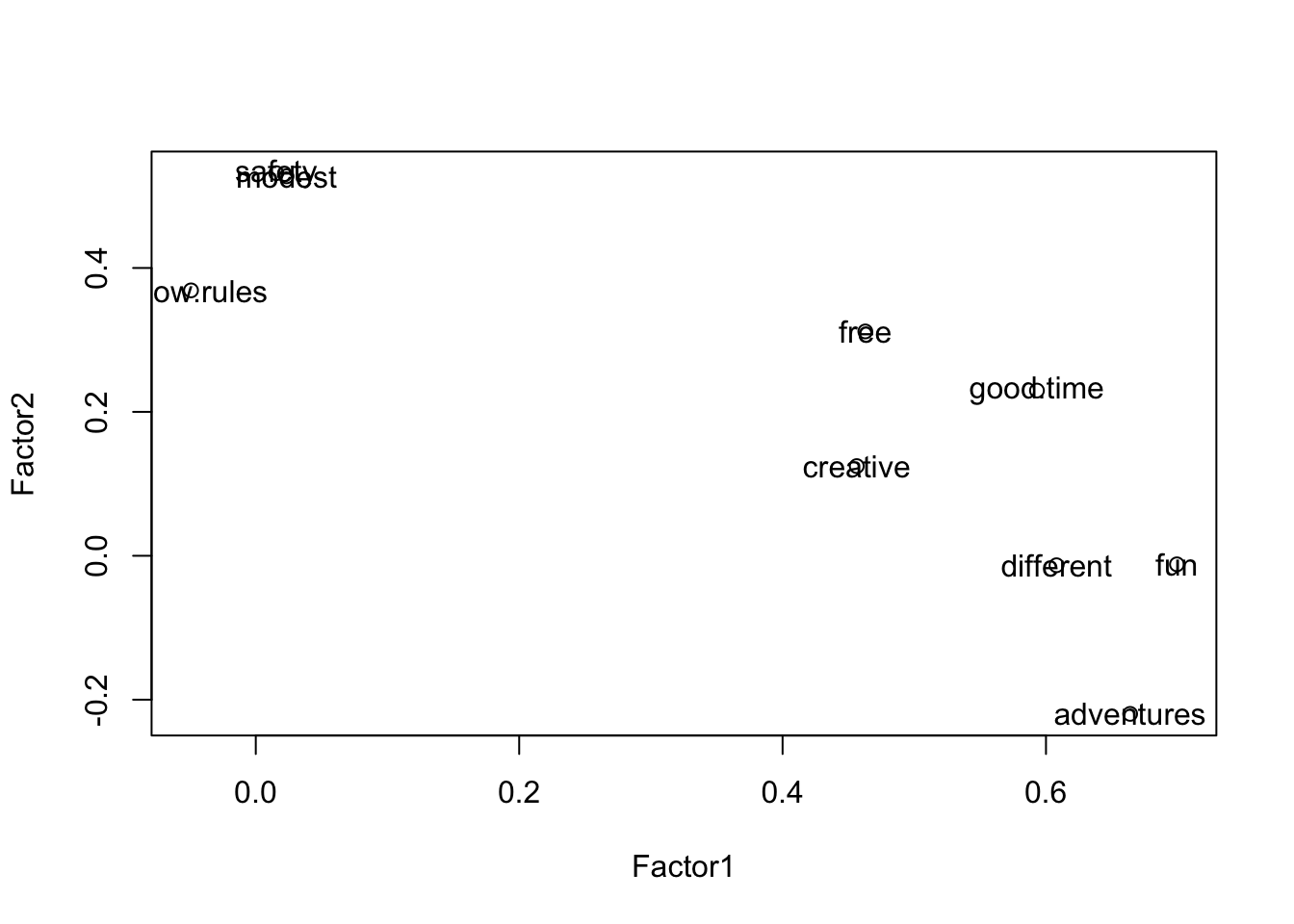

Итак, первый фактор отражается в индикаторах creative, adventures, different и good.time (латентная переменная «Творчество и открытость») - те, для кого важна свобода, креативность, поиска приключений, нового, стремление к веселью и хорошему времяпрепровождению обладают одной общей для них ценностью, связанной с открытостью новому опыту. Второй фактор имеет нагрузки таких индикаторов как follow.rules, modest, safety, то есть важность следования правилам, скромности и безопасности, она, напротив, отражает тенденцию к сохранению. Назоваем этот фактор “Сохранение”.

Однако это не исключает возможности присутствия и трехфакторного решения, альтернативную гипотезу можно сформулировать, используя факторные нагрузки из РФА.

1.7 Альтернативные функции для РФА из пакета psych

# Факторный анализ
fa.values <- fa(PT.values, 
                nfactors = 2, 
                rotate = "geominQ")

# Точечный график с нагрузками двух первых факторов
fa.plot(fa.values)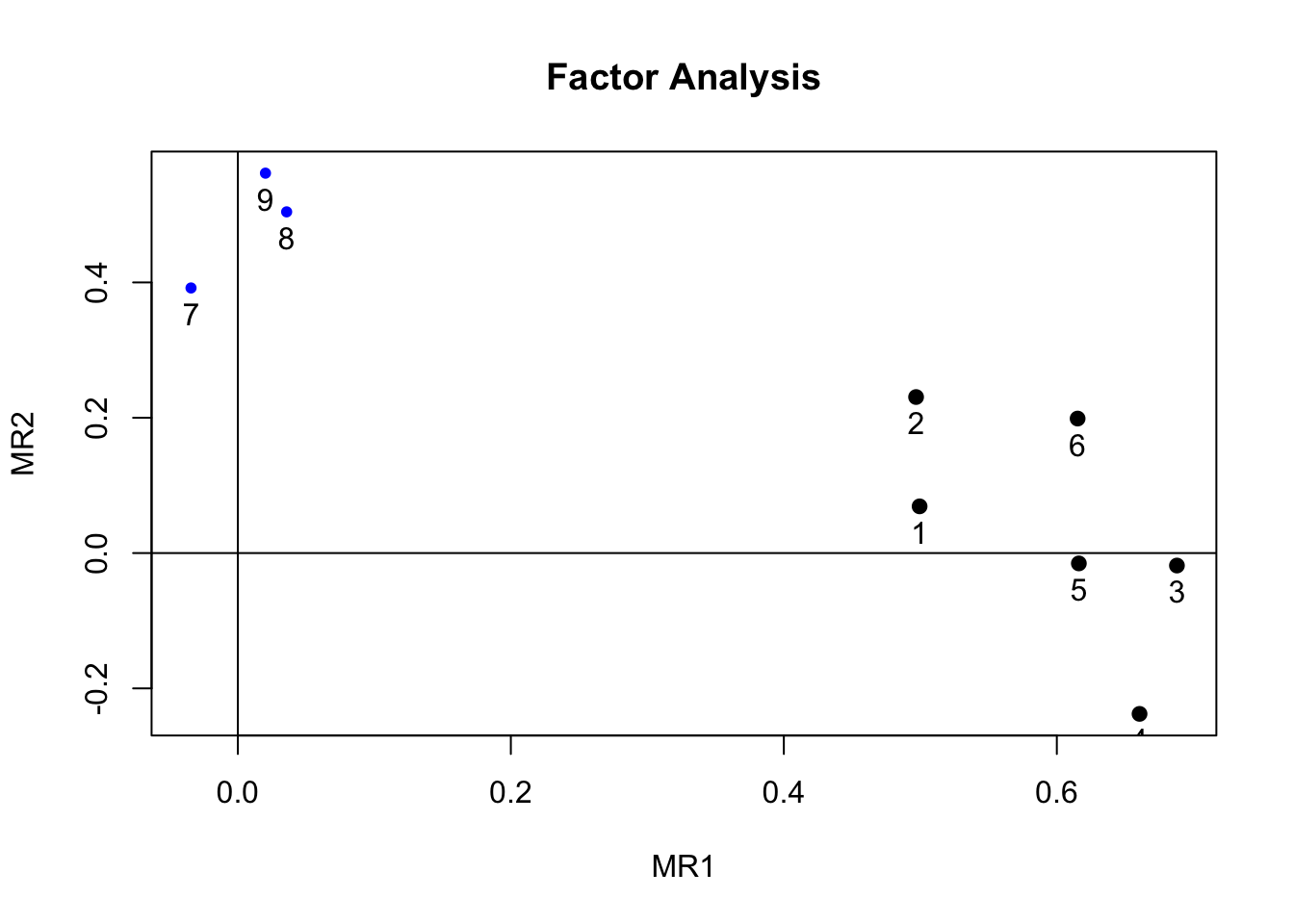

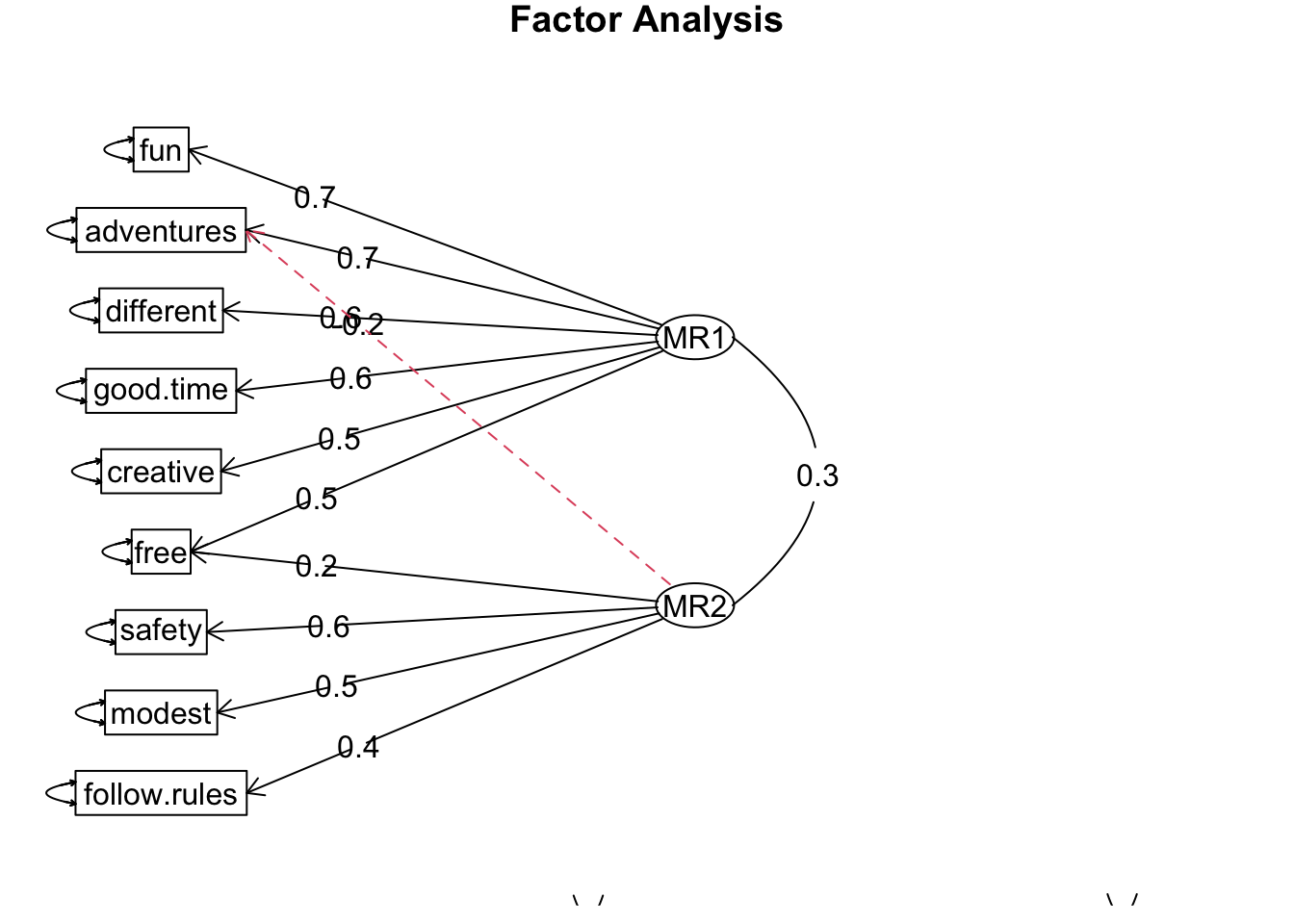
# Диаграмма примерной структуры факторов
fa.diagram( fa.values,  # объект, произведенный функцией fa()
            cut = 0.2, # не показывать нагрузки ниже этого порога
            simple = F, # показывать ли перекрестные нагрузки?
            errors = T  # отображать ли остатки?
           )

2 👉 Самостоятельное задание

На основе индикаторов ценностей, перечисленных ниже, используя разведывательный факторный анализ, найдите оптимальное факторное решение в Германии.

Данные 7 раунда ESS

Используйте код ниже, чтобы переименовать необходимые переменные.

ess7 <- dplyr::rename(ess7, 
                      creative = ipcrtiv,
                      rich = imprich,
                      equality  = ipeqopt,
                      abilities = ipshabt,
                      safety = impsafe,
                      curiosity = impdiff,
                      rules = ipfrule,
                      understanding = ipudrst,
                      modesty = ipmodst,
                      pleasure = ipgdtim,
                      freedom = impfree,
                      helping = iphlppl,
                      success = ipsuces,
                      government = ipstrgv,
                      adventures = ipadvnt,
                      conformity = ipbhprp,
                      respect = iprspot,
                      friends = iplylfr,
                      environment = impenv,
                      traditions = imptrad,
                      hedonism = impfun )

Итоговый список необходимых переменных: c("ipcrtiv", "imprich", "ipeqopt", "ipshabt", "impsafe", "impdiff", "ipfrule", "ipudrst", "ipmodst", "ipgdtim", "impfree", "iphlppl", "ipsuces", "ipstrgv", "ipadvnt", "ipbhprp", "iprspot", "iplylfr", "impenv", "imptrad", "impfun")

Шаги:

  1. Определите количество факторов.

  2. В выбранном факторном решении выберите метод вращения, примените его и рассмотрите нагрузки и показатели качества модели.

  3. Сделайте содержательный вывод.

  4. Возможны ли альтернативные решения?



Максим Руднев, 2018-2021 на основе RMarkdown.