Латентные переменные

Наблюдаемые vs Латентные переменные

Резонно ли допущение о том, что конструкт измерен безошибочно?

Зависит от полноты имеющейся информации об изучаемом конструкте.

В каждом отдельном случае зависит от надежности и валидности измерительных инструментов.

* Рост
* Пол
* Возраст
* Образование
* Социально-экономический статус
* Доверие парламенту
* Субъективное благополучие
* Потребительская привлекательность продукта

Даже в случае переменной «рост» лучше применять многоиндикаторное измерение конструкта (например, утром, днем и вечером).

Латентная переменная - это

Явление, которое нельзя наблюдать непосредственно.
Ожидаемое значение наблюдаемой переменной (очищенное от ошибки, «истинное значение» либо latent response model).
Вообще любая переменная, для которой нет значений в данных (Боллен).
Все, что есть общего у индикаторов (аксиома локальной независимости).

Типы латентных переменных

Априорные и апостериорные (есть ли в существующей теории)
Рефлективные - где индикаторы являются следствиями лат.переменных vs. формативные, где индикаторы - причины
Интервальные или категориальные (факторы vs. кластеры)
Идентифицированные и неидентифицированные (есть ли шанс их измерить).

Измерение латентных переменных

Виды моделей с латентными переменными

Линейные регрессии (остаток)
Мультиномиальные регрессии (преобразованная зависимая переменная)
Факторный анализ (факторы)
Модели латентного роста (кривая роста)
Анализ латентных классов (классы/кластеры)
Item Response Theory - современная теория тестов (ability, «способность»)
Структурные модели с латентными переменными

Модель общего фактора Терстоуна

Цель факторного анализа – найти параметры латентной(ых) переменной(ых), которые объясняют всю* корреляцию/ковариацию между всеми переменными-индикаторами через расщепление дисперсии индикаторов на общую и уникальную.*

Терстоун

Каждый индикатор является линейной функцией одного или более факторов и уникальных дисперсий индикаторов.

То же, в виде факторного анализа .

Анализ (метод) главных компонент не является факторным анализом

потому что

не расщепляет дисперсию наблюдаемых переменных на общую (фактор) и уникальную (остатки);
ошибка измерения/модели не берется в расчет;
ищет такие веса собственных значений (компоненты weigenvalues), при учете которых дисперсии индикаторов максимально объясняются; в факторном анализе целью является объяснение ковариаций;

АГК предназначен для сокращения размерности данных.

Типичный пример: сжатие изображений. Чтобы сохранить максимум информации об изображении, но существенно сократить информацию о каждом пикселе.

Может работать с небольшими выборками.
Не требует теории о латентной переменной,
~~Не подходит для индикаторов, которые слабо друг с другом связаны.~~
~~Плохо подходит для случаев, когда планируется дальнейшее проведение КФА.~~

КФА

Модели конфирматорного и разведывательного ФА

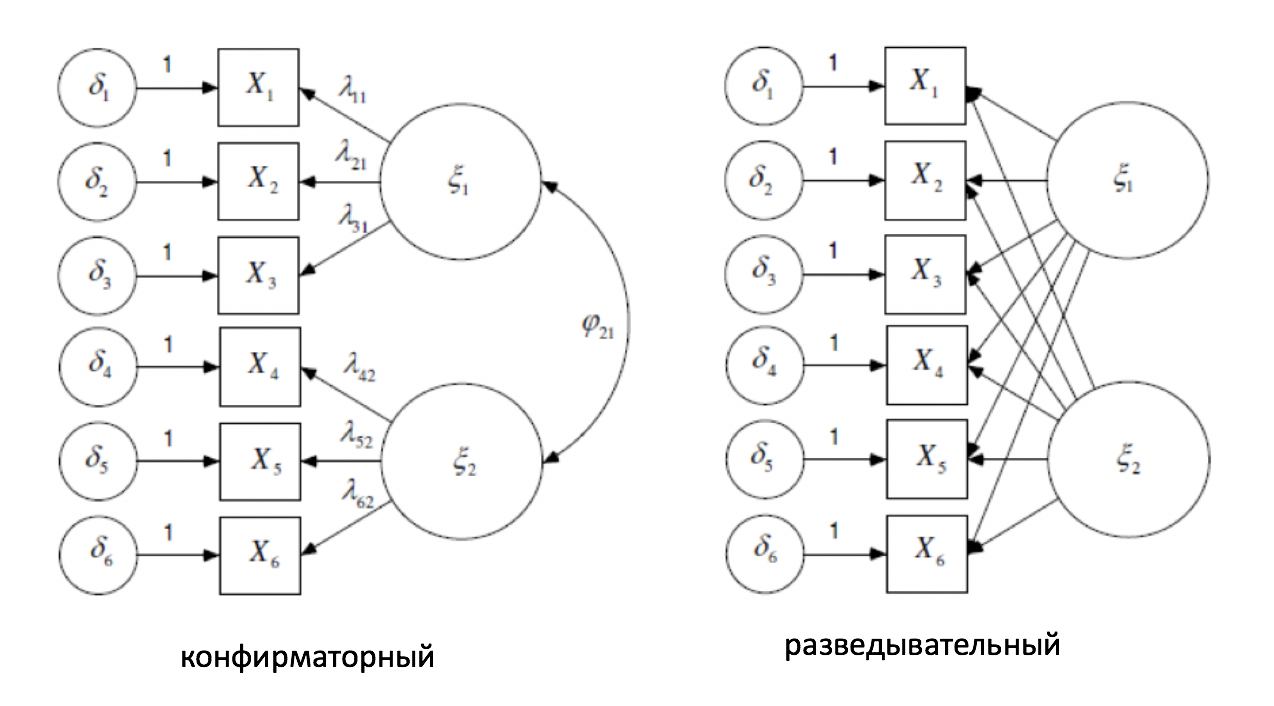
В отличие от разведывательного, конфирматорный ФА:

Следует правилу экономности, используя меньшее количество параметров;
Пересекающиеся нагрузки (cross-loadings) исходно зафиксированы равными нулю (но можно и отменить эту фиксацию);
Вращение не требуется, т.к. более простая структура достигается за счет фиксации параметров;
Позволяет включать корреляции между остатками индикаторов;
Позволяет проверять различные гипотезы через сравнение моделей.

Различия факторных анализов

Разведывательный	Подтверждающий/Конфирматорный
(Exploratory FA – EFA)	(Confirmatory – CFA)
Нет предварительной теории.	Теория существует.
Отталкиваемся от того, что подсказывают данные.	Исходим из теории и подхода проверяющего гипотезы.
Цель – описание данных.	Цель – проверка гипотез о генсовокпуности.
Количество факторов неизвестно.	Количество факторов известно априори.
Используется на ранних стадиях разработки измерительных шкал.	На поздних стадиях, когда набор индикаторов и их принадлежность к различным факторам уже известна.
Нагрузки всех индикаторов на все факторы устанавливаются свободно (сложности интерпретации)	Нагрузки некоторых индикаторов на соответствующие факторы, остальные нагрузки фиксируются равными нулю

Допущение о локальной независимости

Вся общая ковариация, которая есть у индикаторов одного фактора – является проявлением влияния этого фактора.

Локальная независимость - нескоррелированность индикаторов после “вычитания” из них фактора.

Однако у групп индикаторов могут быть и другие источники ковариации, такие как:

Метод опроса;
Формат вопроса;
Формулировка вопроса;
Источник данных;
Последовательность вопросов;
Содержание (указывает на дополнительный фактор).

Уникальные дисперсии индикаторов могут быть скоррелированы только в КФА

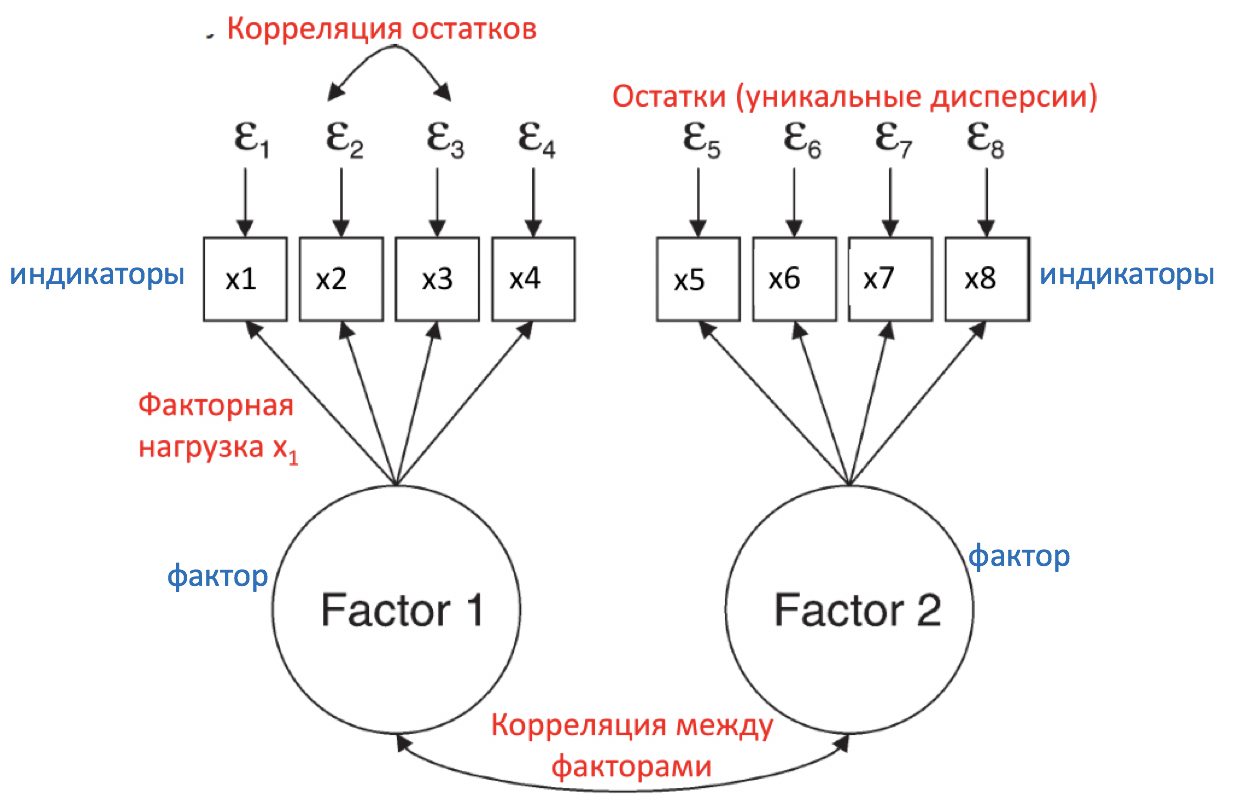
Уравнения и идентификация КФА

Основные уравнения КФА

~~Дисперсия индикатора~~ = факторная нагрузка в квадрате X на дисперсию фактора + остаток. \[ Var(y_1) = F.loading_{y_1}*F.loading_{y_1} * Var_{F_1} + Residual_{y_1} \]

~~Ковариация~~ между двумя индикаторами одного фактора = произведение нагрузок этих индикаторов и дисперсии этого фактора. \[ Covar_{y_1, y_2} = F.loading_{y_1}*F.loading_{y_2}*Var_{F}\] Ковариация между двумя индикаторами одного фактора, между остатками которых ~~разрешена ковариация~~ = произведение нагрузок этих индикаторов, дисперсии фактора плюс ковариация остатков. \[ Covar_{y1,y2} = F.loading_{y_1}*F.loading_{y_2}*Var_{F}+Covar_{Residuals(y_1,y_2)} \]

Ковариация между двумя индикаторами ~~разных~~ факторов = произведение нагрузок этих индикаторов и ковариации между факторами \[ Covar_{y1(F1),y3(F2)} = F1.loading_{y1} * F2.loading_{y3} * Covar_{F1,F2} \]

Пример вычисления

ess7 <- haven::read_sav("data/ESS7e02_1.sav")
Austria <- ess7[ess7$cntry == "AT",]


library(lavaan)
cfa1 <- cfa( 'F1 =~ ipadvnt + impfun + impdiff + ipgdtim;
             F2 =~  ipcrtiv+ impfree;
             impfun ~~ ipgdtim;
             ', data=Austria)

semPlot::semPaths(cfa1, whatLabels="est", style="lisrel", layout="tree2", rotation=2, sizeMan=10, nCharNodes=0, edge.label.cex=1.1)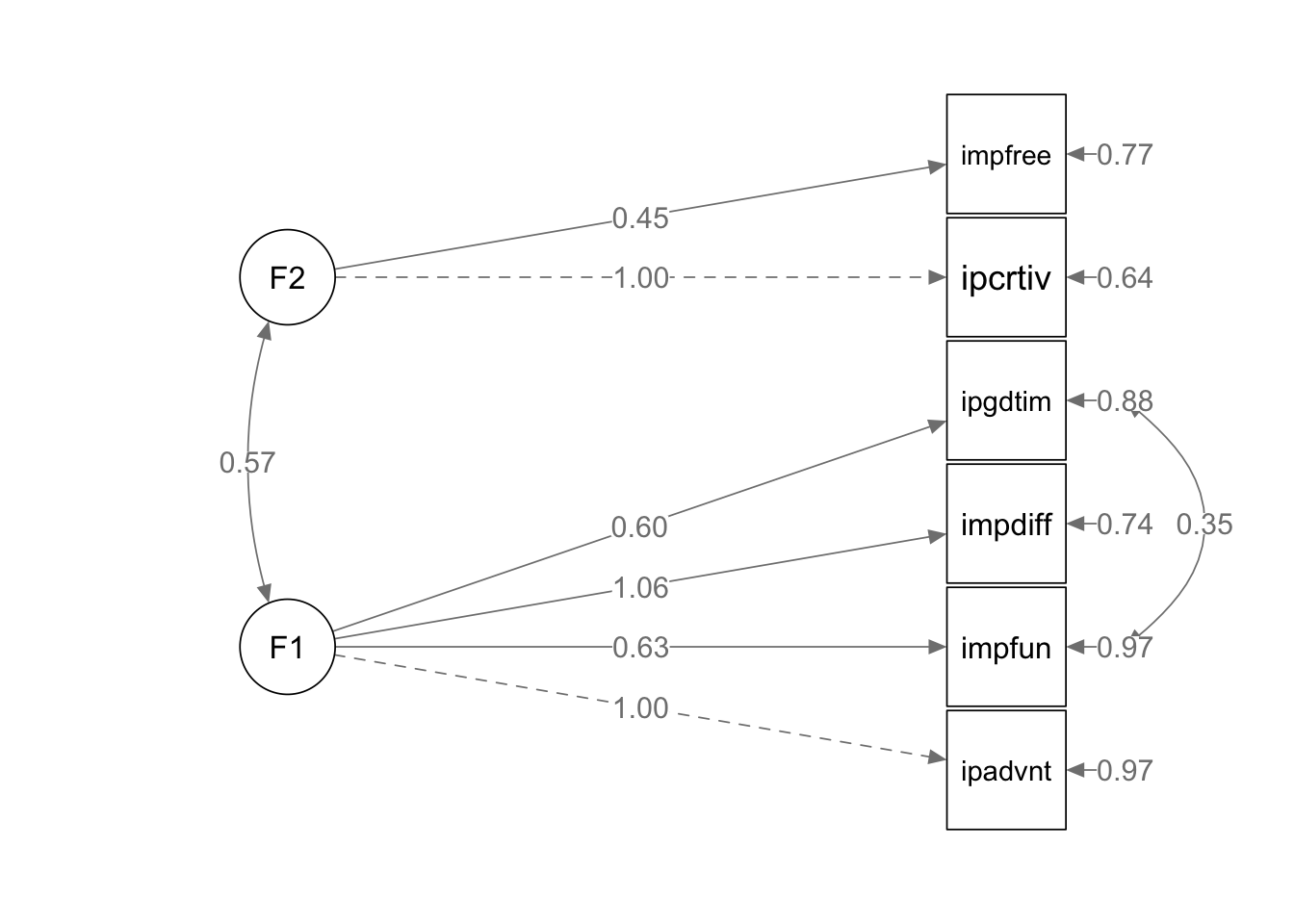

lavInspect(cfa1, "cov.ov") # предсказанная моделью матрица дисперсий-ковариаций

##         ipdvnt impfun impdff ipgdtm ipcrtv impfre
## ipadvnt 1.867                                    
## impfun  0.568  1.333                             
## impdiff 0.947  0.601  1.743                      
## ipgdtim 0.536  0.687  0.567  1.201               
## ipcrtiv 0.569  0.361  0.602  0.341  1.480        
## impfree 0.257  0.163  0.272  0.154  0.379  0.938

Идентификация структурных моделей

\(df≥0\): количество степеней свободы должно быть равно или больше нуля;

\(df = N_{obs} – N_{par}\): кол-во степеней свободы – это разница между количеством уникальных элементов матрицы дисперсии-ковариации наблюдаемых переменных и количеством параметров в модели;

\(N_{obs} = (N_{vars}(N_{vars} + 1))/2\): количество уникальных элементов матрицы дисперсии-ковариации;

\[Npar_{FA} = (N_{fact} * (N_{fact}+1))/2 + N_{vars}*N_{fact} + N_{vars} – N_{fact}\]

Количество параметров в факторном анализе включает:

дисперсии и ковариации факторов Nfact*(Nfact+1))/2,
остатки наблюдаемых переменных Nvars,
факторные нагрузки Nvars * Nfact,
исключает зафиксированные параметры Nfact (фиксируется либо дисперсия фактора = 1, либо одна из нагрузок в каждом факторе = 1).

Идентификация: простые правила

В КФА:

Df≥0
Каждой латентной переменной (включая остатки) должная быть приписана метрика: Дисперсии факторов или одна нагрузка на каждый из факторов должны быть зафиксированы (обычно равными 1)
В случае однофакторной модели – не менее 3-х индикаторов.
3 индикатора на фактор рекомендованы и для других КФА.

В путевом анализе/структурной части:

все путевые модели, не включающие циклов идентифицированы.

Как выбирать метрику для латентной переменной (фактора)?

Нужно взять индикатор, обладающий известными характеристиками, наиболее надежный и валидный, т.е. именно он будет задавать «единицу измерения» латентной переменной (фактора)

1

2

3 Не идентифицированная - 1

-1 степень свободы

Не идентифицированная - 2

-1 степень свободы

Проверка гипотез в КФА

Фиксирование параметров

назначение априорного значения (обычно 1 или 0) одному из искомых параметров.

По сути зафиксированный параметр не является параметром (т.е. искомым), поскольку его значение определено априорно.

Используется

для сокращения количества параметров в модели с целью идентифицировать модель;
для проверки гипотез о равенстве 0 (или любому другому значению).

Ограничение параметров

ограчение диапазона возможных значений параметра через математическое выражение и отношения с другими параметрами.

Например, можно ограничить два параметра выражением равенства, т.е. назначить их равными друг другу.

Фиксирование и ограничение параметров для проверки гипотез

Сравнение вложенных моделей с зафиксированными/ограниченными vs. свободными параметрами.

Например:

Нагрузки всех индикаторов равны;
Нагрузки некоторых индикаторов равны нулю;
Нагрузки индикаторов равны в различных выборках;
Двухфакторная модель лучше трехфакторной;
Проверка допущения о нескоррелированности остатков.

Являются вложенными

две модели, одна из которых может быть получена посредством фиксации или ограничения параметров другой.

В КФА:

Одно- и двухфакторная модель при условии неизменности остальных параметров (аналогично фиксированию корреляции между факторами 1)
Модель с фактором второго порядка и обычный КФА с факторами, корреляции между которыми не зафиксированы равными нулю.
Тест разницы хи-квадратов применим только для вложенных моделей.

Не являются вложенными

Модели, в которых одновременно исключаются и включаются различные параметры.
- При условии сохранения набора наблюдаемых переменных, такие модели можно сравнивать с помощью AIC и BIC (более низкие значения указывают на более подходящую модель).
Модели, в которых различаются наборы наблюдаемых переменных
- Для таких моделей НЕ СУЩЕСТВУЕТ статистически обоснованных критериев сравнения. Процесс модификации модели в этом случае обрывается и запускается новый цикл поиска модели.

Примеры

Полная

Вложенная

Оценка согласия модели

Предсказанная и наблюдаемая матрица дисперсий-ковариаций

# Наблюдаемая матрица дисперсий-ковариаций
observed.var.cov <- cov(Austria[,c("ipadvnt", "impfun", "impdiff", "ipgdtim", "ipcrtiv", "impfree")], use="complete.obs")

round(observed.var.cov,2)

##         ipadvnt impfun impdiff ipgdtim ipcrtiv impfree
## ipadvnt    1.87   0.63    0.96    0.52    0.50    0.18
## impfun     0.63   1.33    0.56    0.69    0.32    0.21
## impdiff    0.96   0.56    1.74    0.53    0.65    0.25
## ipgdtim    0.52   0.69    0.53    1.20    0.40    0.33
## ipcrtiv    0.50   0.32    0.65    0.40    1.48    0.38
## impfree    0.18   0.21    0.25    0.33    0.38    0.94

# Предсказанная моделью
implied.var.cov <- lavInspect(cfa1, "cov.ov")
implied.var.cov

##         ipdvnt impfun impdff ipgdtm ipcrtv impfre
## ipadvnt 1.867                                    
## impfun  0.568  1.333                             
## impdiff 0.947  0.601  1.743                      
## ipgdtim 0.536  0.687  0.567  1.201               
## ipcrtiv 0.569  0.361  0.602  0.341  1.480        
## impfree 0.257  0.163  0.272  0.154  0.379  0.938

# Разница между предсказанной и наблюдаемой матрицами дисперсий-ковариаций (матрица остатков)
implied.var.cov - observed.var.cov

##         ipdvnt impfun impdff ipgdtm ipcrtv impfre
## ipadvnt -0.001                                   
## impfun  -0.067 -0.001                            
## impdiff -0.017  0.037 -0.001                     
## ipgdtim  0.012  0.000  0.036 -0.001              
## ipcrtiv  0.065  0.045 -0.044 -0.055 -0.001       
## impfree  0.072 -0.045  0.023 -0.175  0.000 -0.001

GFI

Goodness of Fit index

Рекомендованные значения: >0.90

Индекс абсолютного согласия – доля ковариаций, объясненных моделью (сравнивает модель с параметрами и «нулевую» модель без параметров совсем),

\[GFI = 1 – \frac{сумма~квадратов ~остатков}{сумма ~квадратов ~наблюдаемой ~матрицы ~дисперсии/ковариации}\]

Зависит от размера выборки (положительно связан)

SRMR

Standardized Root Mean Square Residual

Рекомендованные значения: <0.08

Усредненный остаток (сравниваются предсказанная моделью матрица корреляций и реальная)
- Некоторые остатки могут быть высокими, и это не будет отражено в SRMR, поэтому лучше рассматривать матрицы остатков самостоятельно

residuals(path1, type="standardized")`

Два разных хи квадрата

Хи-квадрат тестируемой модели [Chi-Square Test of Model Fit /Minimum Function Test Statistic] - сравнивает предсказанную нашей моделью матрицу ковариаций и эмпирическую матрицу ковариаций.

\[\chi^2 = F_{ML}*(N-1)~ при~ df_M\] где \(F_{ML}\) - значение функции правдоподобия, \(N\) – размер выборки.

Хи-квадрат модели независимости [Baseline Model/Independence model] - сравнивает матрицу, предсказанную моделью независимости и эмпирическую матрицу ковариаций.

CFI

Comparative Fit index

Рекомендованные значения: >0.90 или >0.95

Сравнительный индекс, сравнивает согласие тестируемой модели и «базовой» модели независимости с эмпирической матрицей дисперсии-ковариации.

Базовая модель маловероятна, поэтому значения обычно очень высоки.

\[ CFI = 1- \frac{\chi^2_{model}-df_{model}}{\chi^2_{independence}-df_{independence}}\]

TLI

Tucker-Lewis Index

Рекомендованные значения: >0,90 или >0,95.

По смыслу похожа на CFI.

Иногда превосходит 1.

\[ TLI = \frac{\frac{\chi^2_{independence}}{df_{independence}} - \frac{\chi^2_{model}}{df_{model}}}{ \chi^2_{independence}/df_{independence}-1 }\]

RMSEA

Root Mean Squared Error of Approximation

Рекомендованные значения: <0.08

PCLOSE – вероятность близости RMSEA к 0,05

Чем выше значения RMSEA, тем НИЖЕ согласие модели.

Наказывает за большее количество параметров.

\[ RMSEA = \sqrt\frac{\chi^2_{model} - df_{model}}{df_{model}*(N-1)} \] Лучше других работает на больших выборках.

Следует уделять внимание доверительному интервалу RMSEA

Демонстрируйте все показатели согласия

так как все они имеют свои недостатки и в одиночестве могут ввести вас и читателя в заблуждение относительно модели.

Обычные (стандатизованные) остатки – также важный критерий согласия модели, указывающий на локальные источники ошибки.

Информационные критерии для сравнения невложенных моделей

хи-квадрат модели с поправкой на сложность модели, размер выборки и количество переменных

❗️ По-разному вычисляются в разных программах. Годятся только для сравнения моделей, вычисленных одной программой. Не несут содержательного смысла сами по себе.

Akaike Information Criterion - AIC \[ AIC = χ^2 - 2*df \]

Bayesian Information Criterion - BIC \[ BIC = χ^2+\log(N_{samp})*(N_{vars}(N_{vars} + 1)/2 – df) \]

The Sample-Size Adjusted BIC \[ SABIC = χ^2 +[(N_{samp} + 2)/24]*[N_{par}*(N_{par} + 1)/2 - df] \]

Expected Cross-Validation Index \[ ECVI = \frac{χ^2}{N-1} + \frac{2*N_{par}}{N-1} \]

\(df\) -количество степеней свободы

\(N_{vars}\) – количество переменных в модели

\(N_{par}\) – количество свободных параметров в модели

\(N_{samp}\) – размер выборки

~~Чем меньше, тем лучше.~~

Все статистики согласия обладают следующими ограничениями

Оценивают согласие всей модели, но не отдельных ее параметров, объединяя «хорошие» результаты и «плохие»
Нет единственного критерия согласия модели, всегда нужно смотреть на несколько критериев
Критерии согласия не указывают на источники низкого (или высокого) качества
Критерии согласия не говорят о предсказательной силе модели для индивидуальных данных (как это делает R2)
Высокие показатели согласия модели не являются гарантией теоретической осмысленности модели

Применение КФА

Валидность и надежность

предмет психометрики/психометрии.

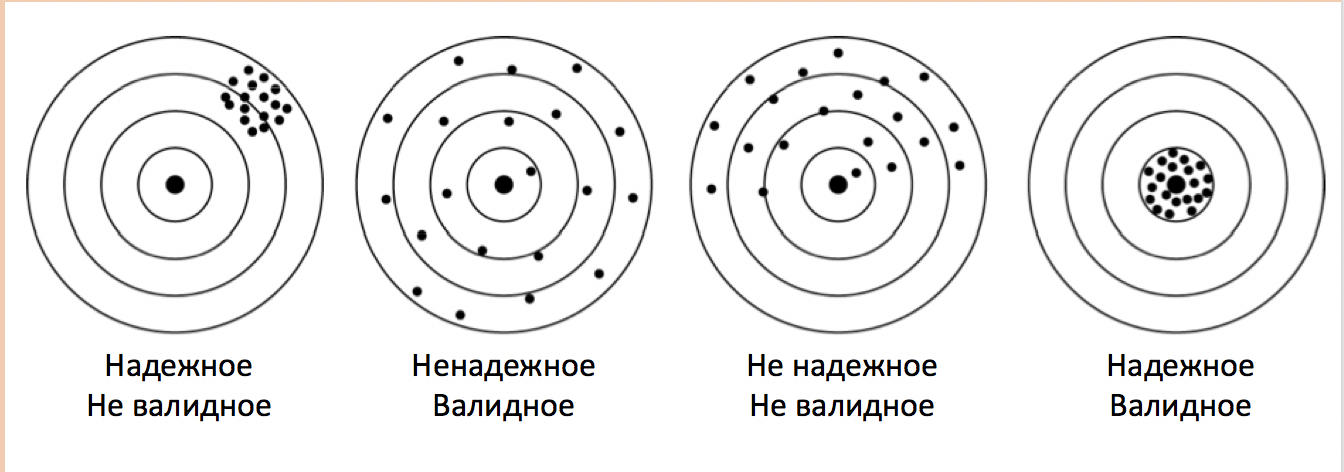
Надежность измерения – насколько точно измерение

Степень, в которой значения переменной свободны от случайно ошибки измерения.

Согласованность (Альфа Кронбаха) – общая скоррелированность между наблюдаемыми переменными
Устойчивость (тест-ретест)
Надежность параллельных форм (различными индикаторами) – сравнение средних/в SEM - латентных средних
DIF - differential item functioning (различное функционирование индикаторов на разных выборках) – специальное применение многогруппового КФА в проверках на инвариантность измерения.
и другие.

Большее количество индикаторов на один концепт помогают повысить надежность измерения. Большее разнообразие индикаторов повышает валидность, так как они охватывают различные аспекты изучаемого явления и единственное, что у них остается общего – это дисперсия самого концепта.

Омега МакДональда: показатель надежности измерения латентной переменной (аналог альфы Кронбаха для КФА)

Более высокие значения соответствуют большей консистентности (однородности) индикаторов. Применим только для ФА с индикаторами на одной шкале.

\[ \omega = \frac{(Сумма~нагрузок)^2}{((Сумма~нагрузок)^2+сумма~остатков (+корр. остатков)}\]

Валидность измерения – измеряет ли инструмент то, что он должен измерять.

Конструктная (измеряет ли то, что должен измерять) – самая важная!
Содержательная (индикаторы покрывают все стороны измеряемого конструкта)
Конвергентная (другой инструмент, измеряющий тот же конструкт, дает такие же результаты), Дивергентная (не коррелирует с конструктом, с которым теоретически не связана)
Дискриминантная (отличается от близких/схожих конструктов)
Критериальная (измерения схожих конструктов связаны с результатами измерения данного)
Предсказательная (предсказывает теоретически возможные исходы)

DIF – differential item functioning

Ситуация, в которой одни и те же индикаторы по-разному работают на разных выборках.
Например, студенты мужского пола обычно лучше справляются с заданиями, в контексте которых есть спорт или техника.

Факторы второго порядка

higher-order factor models

Факторы второго порядка объясняют ковариации между фаткорами первого порядка.

Все правила построения КФА распространяются и на факторы второго порядка.

Структурные модели второго порядка

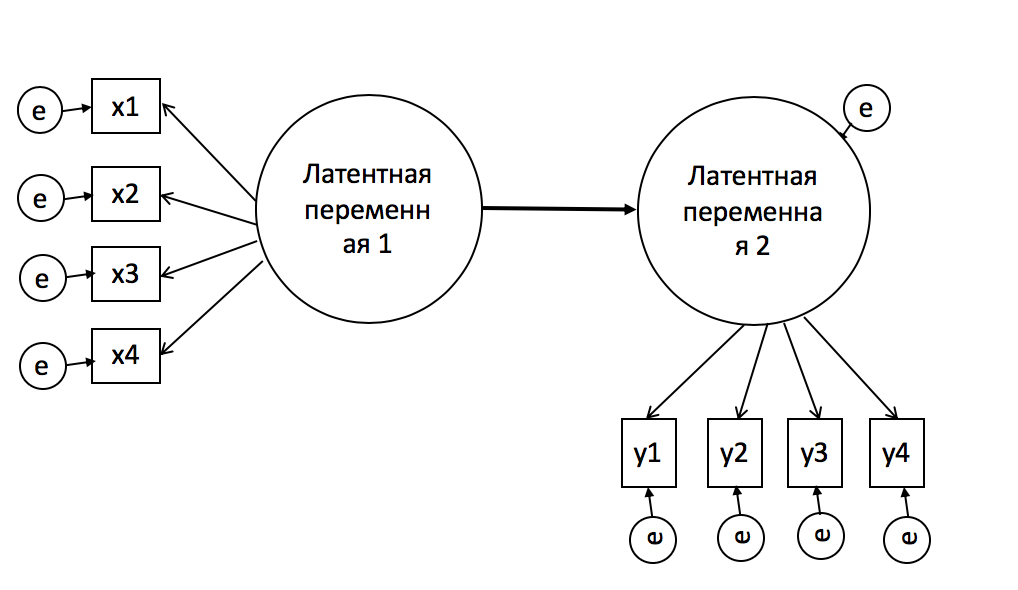
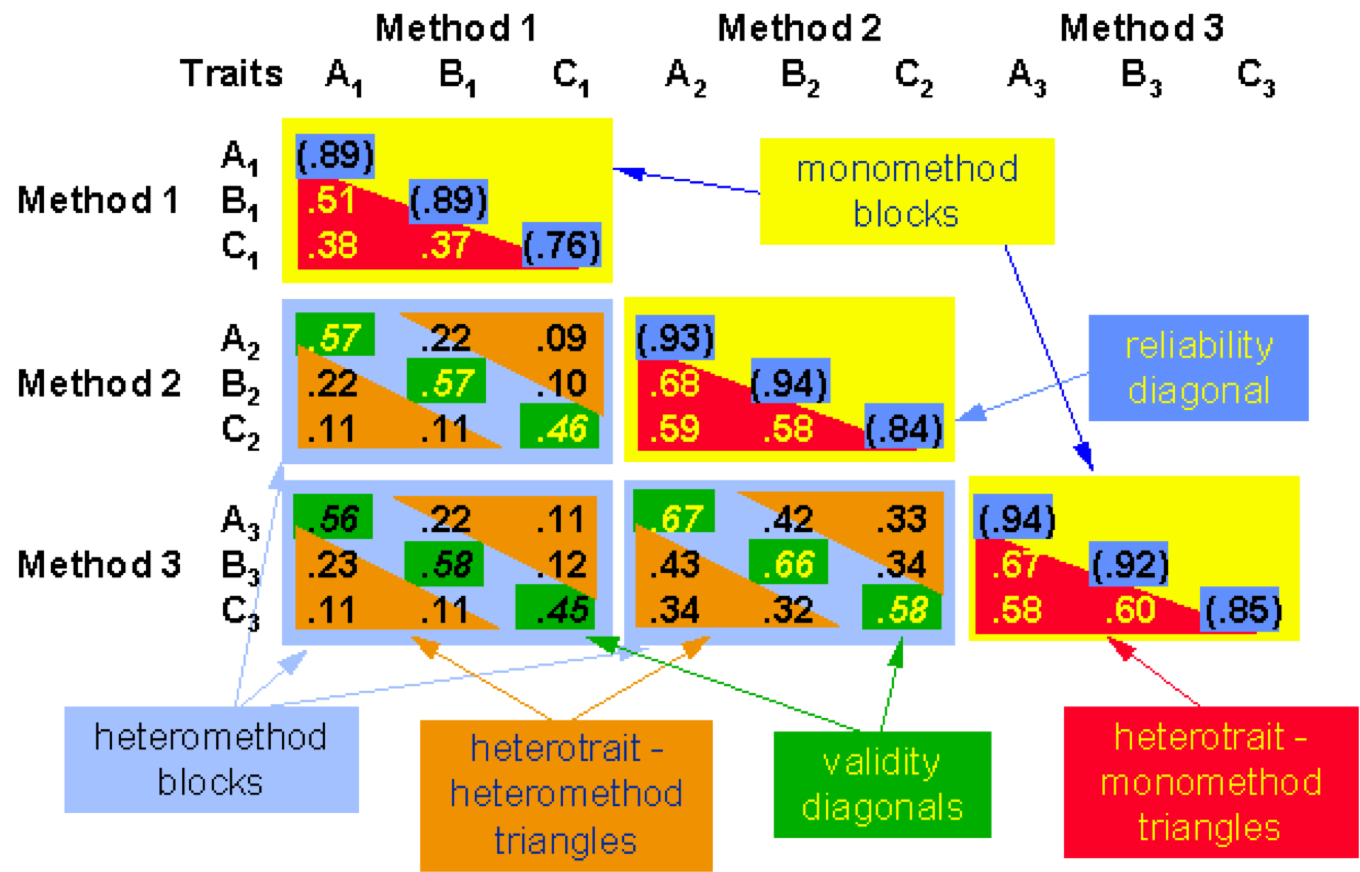
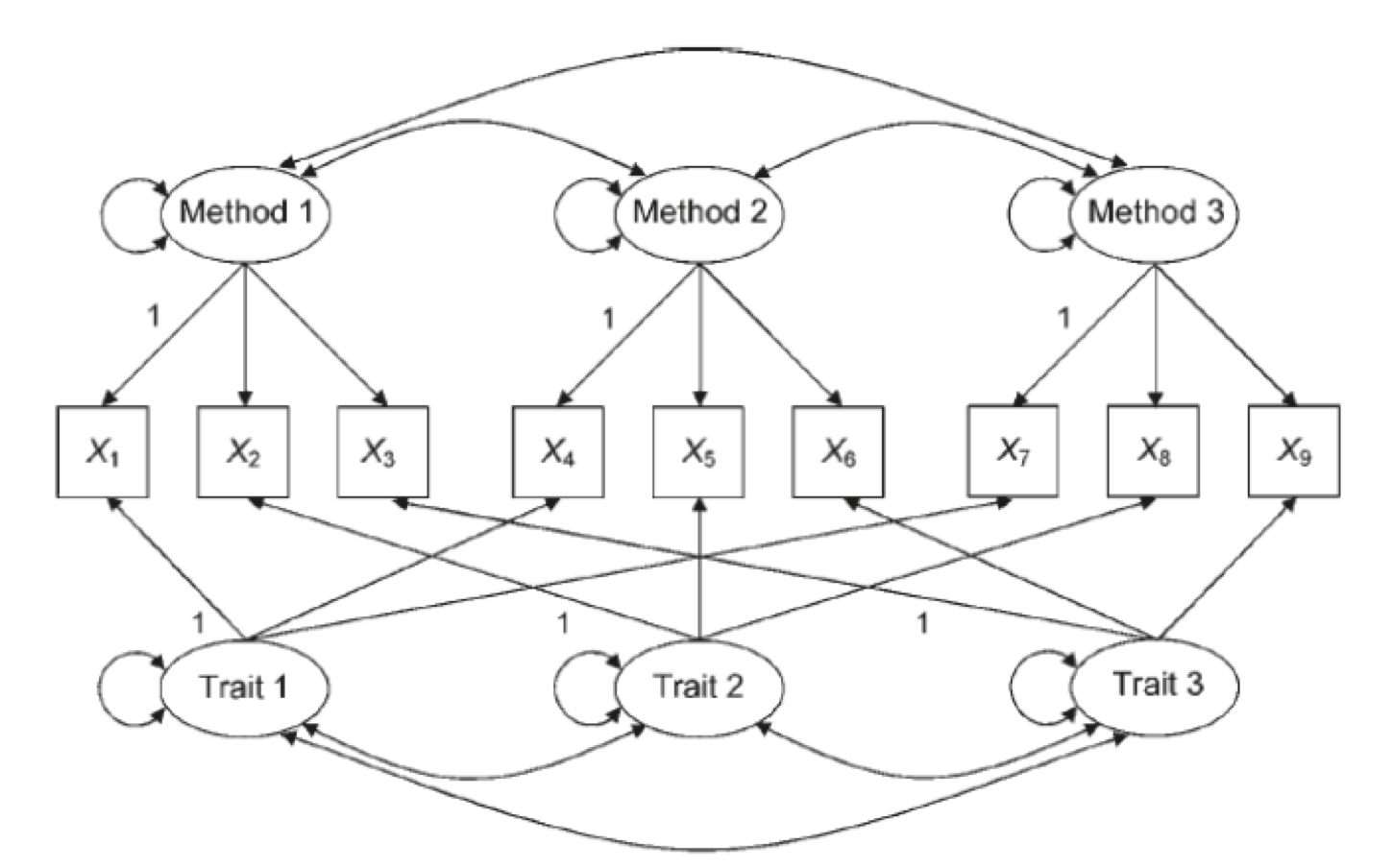
MTMM - Multitrait-multimethod models (MTMM)

Модель множественных латентных переменных при множестве методов
Позволяет оценить конвергентную и дискриминантную валидность измерения латентных переменных

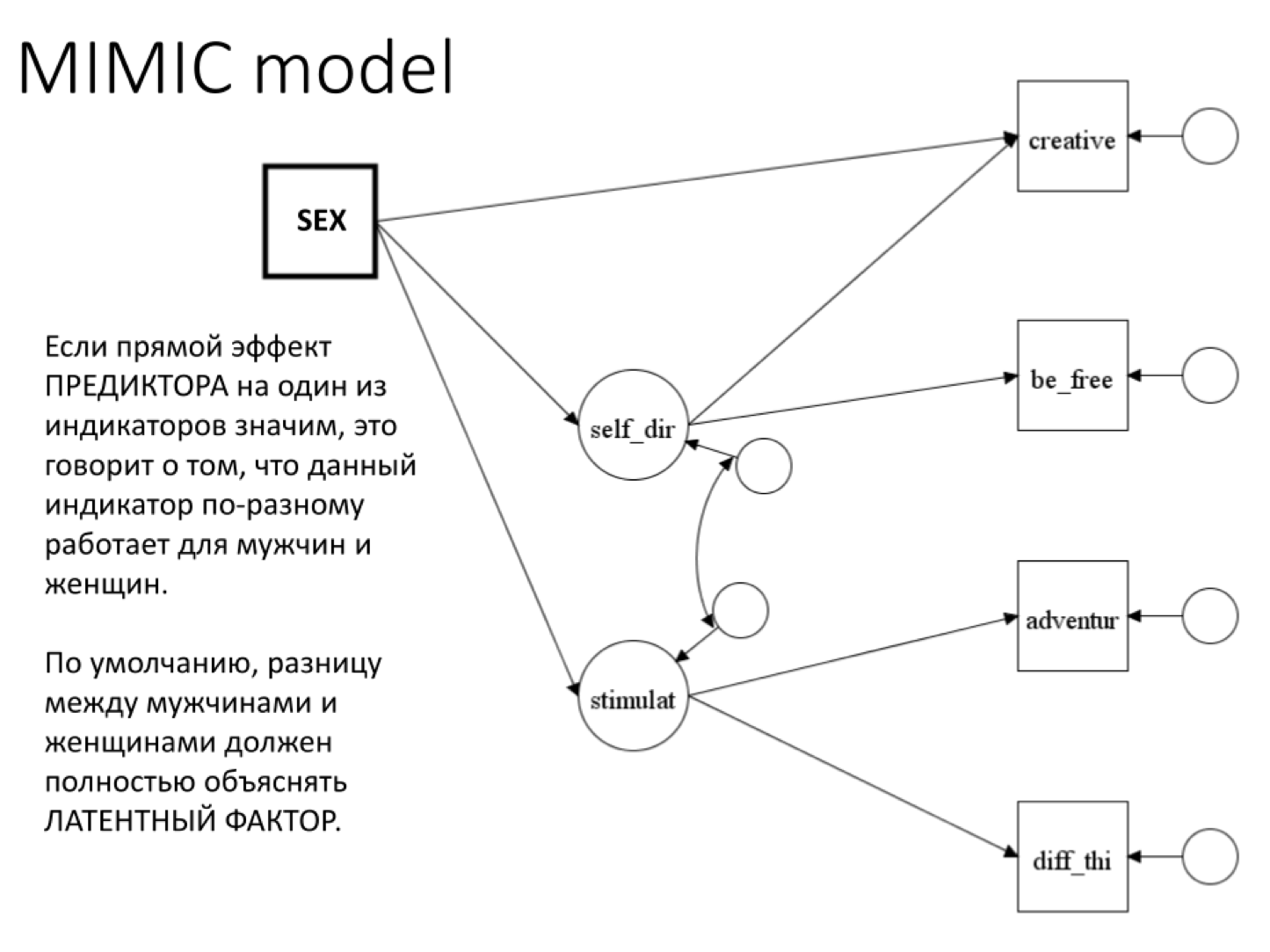
MIMIC - multiple indicators multiple causes

Модели с методическим фактором

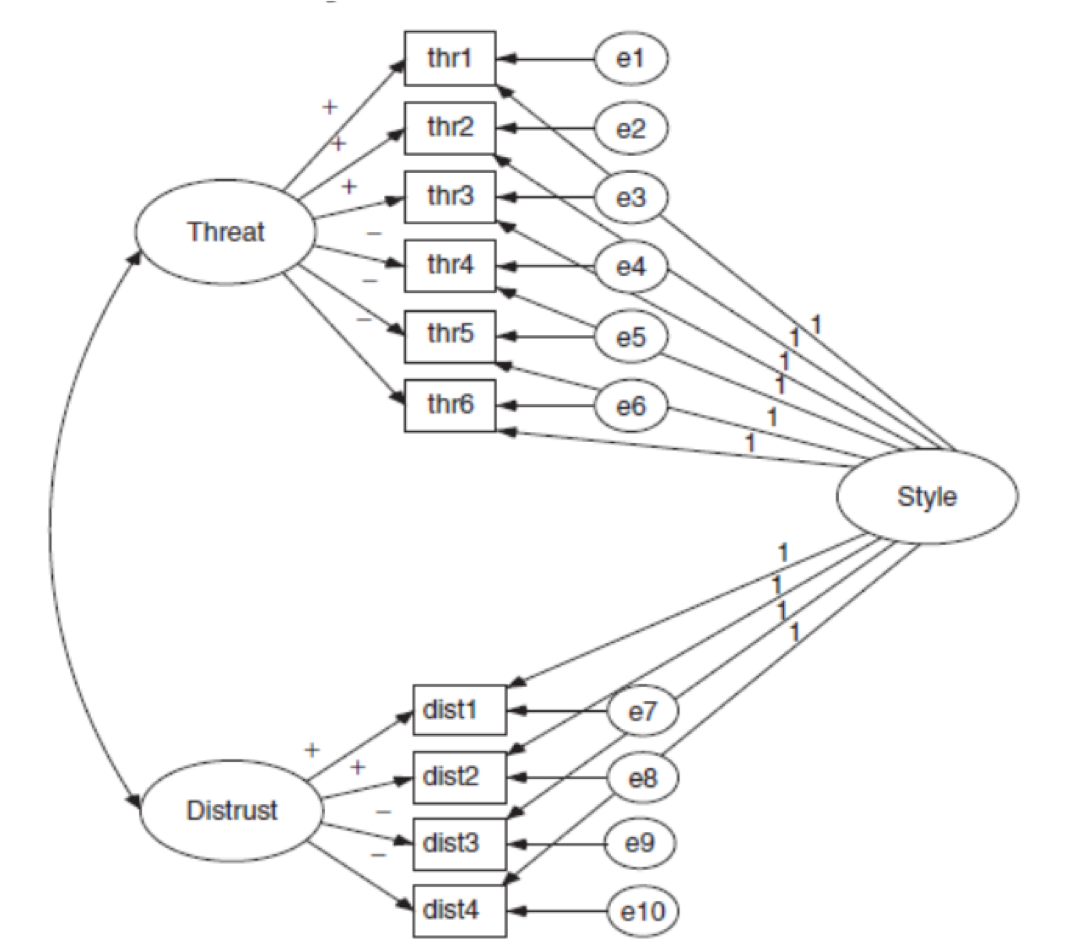
Формативная модель измерения

Примеры:

Социально-экономический статус;
Экономические показатели;
Медицинские;
~~Часто ошибочно используются и в социологии!~~

Проблемы формативной модели

Удаление одного из индикаторов изменяет содержание индекса, т.к. они независимы.
Нет ошибки измерения.
Модель не идентифицирована в терминах структурных уравнений.
Оправдана только тогда, когда есть полная уверенность в том, что индикаторы являются ~~причиной~~ латентной переменной.

Максим Руднев, 2018-2021 на основе RMarkdown.

Лекция 5 – Конфирматорный факторный анализ

22 сентября 2021 г.