Путевой анализ - Path Analysis
16 сентября 2021 г.
1 🤲 Пример разработки модели
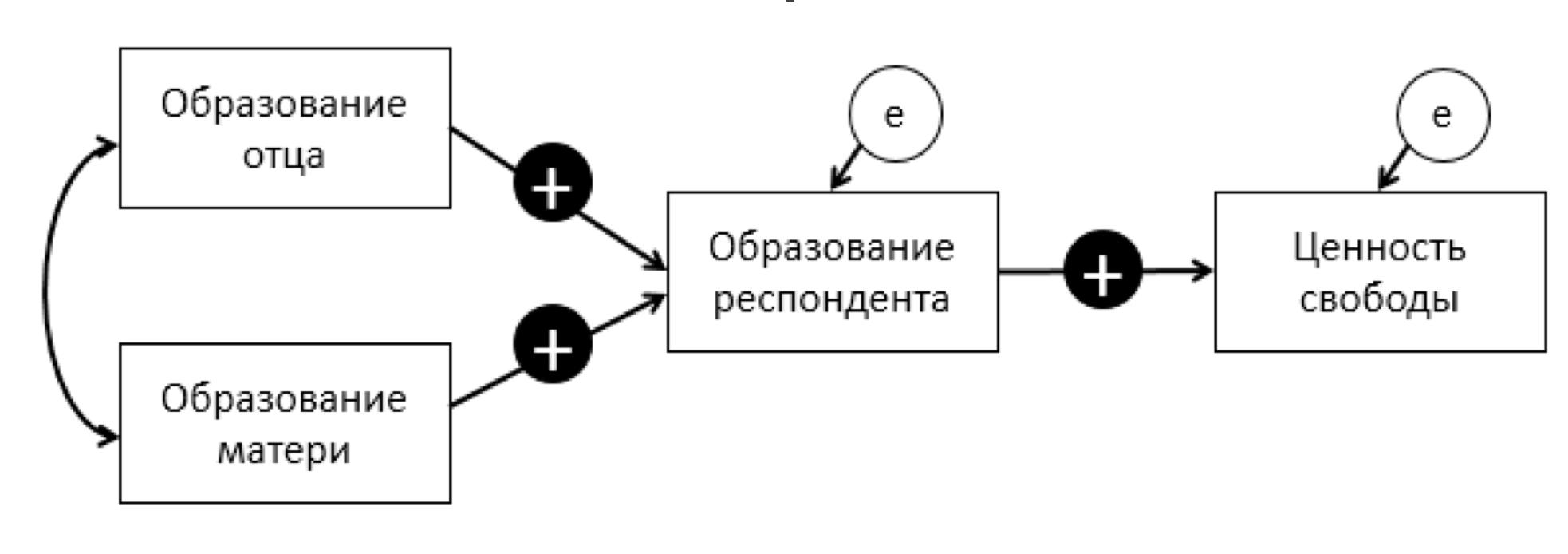
1.1 Теоретическая модель
Основная гипотеза: Влияние образования отца и матери на ценности респондента полностью опосредовано образованием респондента, поскольку именно собственное образование человека является агентом, формирующим ценности свободы. Соответственно, прямое влияние образования родителей на ценность свободы респондента отсутствует.
Дополнительные: Образование отца положительно влияет на образование респондента. Образование матери положительно влияет на образование респондента. Образование респондента положительно влияет на ценность свободы.
Теоретическая модель, построенная на гипотезах, выглядит так:
1.2 Множественная регрессия в lavaan
# Запускаем все необходимые библиотеки для данного семинара
library("lavaan")
library("foreign")
library("semPlot")
# Импортируем данные
ess7 <- read.spss("data/ESS7e02_1.sav",
use.value.labels = F,
use.missings = T,
to.data.frame = T)
# Отбираем австрийцев
Austria <- ess7[ess7$cntry == "AT",]
# Переворачиваем кодировку для ключевой переменной
Austria$impfree.rec <- 7- Austria$impfree
# Подсчитываем регрессию в lavaan
regr <- sem('impfree.rec ~ eduyrs + eiscedf + eiscedm',
data = Austria)
# Запрашиваем результаты анализа
summary(regr)> lavaan 0.6-9 ended normally after 13 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 4
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 0.000
> Degrees of freedom 0
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> impfree.rec ~
> eduyrs 0.029 0.008 3.748 0.000
> eiscedf 0.001 0.011 0.115 0.909
> eiscedm 0.018 0.009 2.113 0.035
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
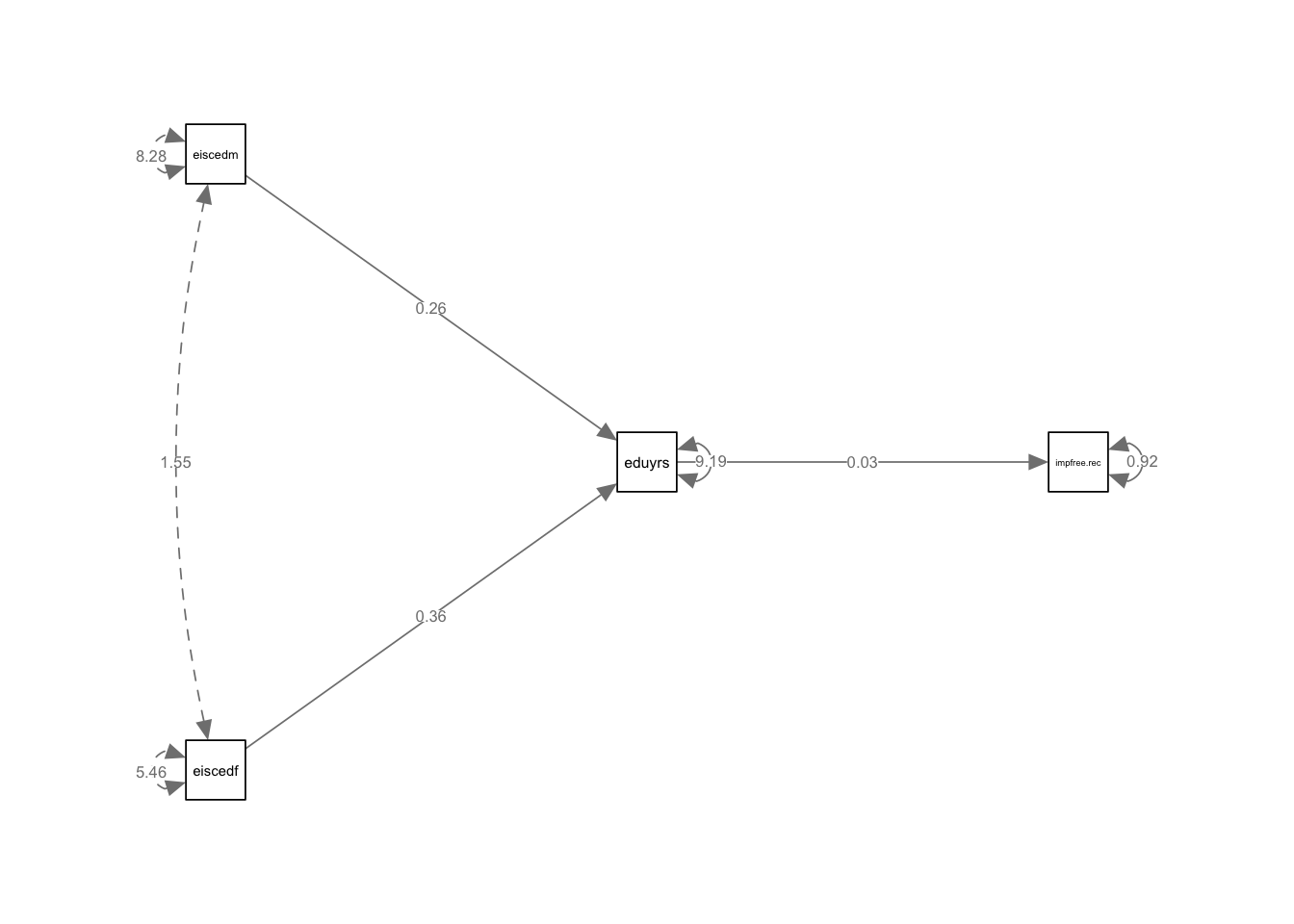
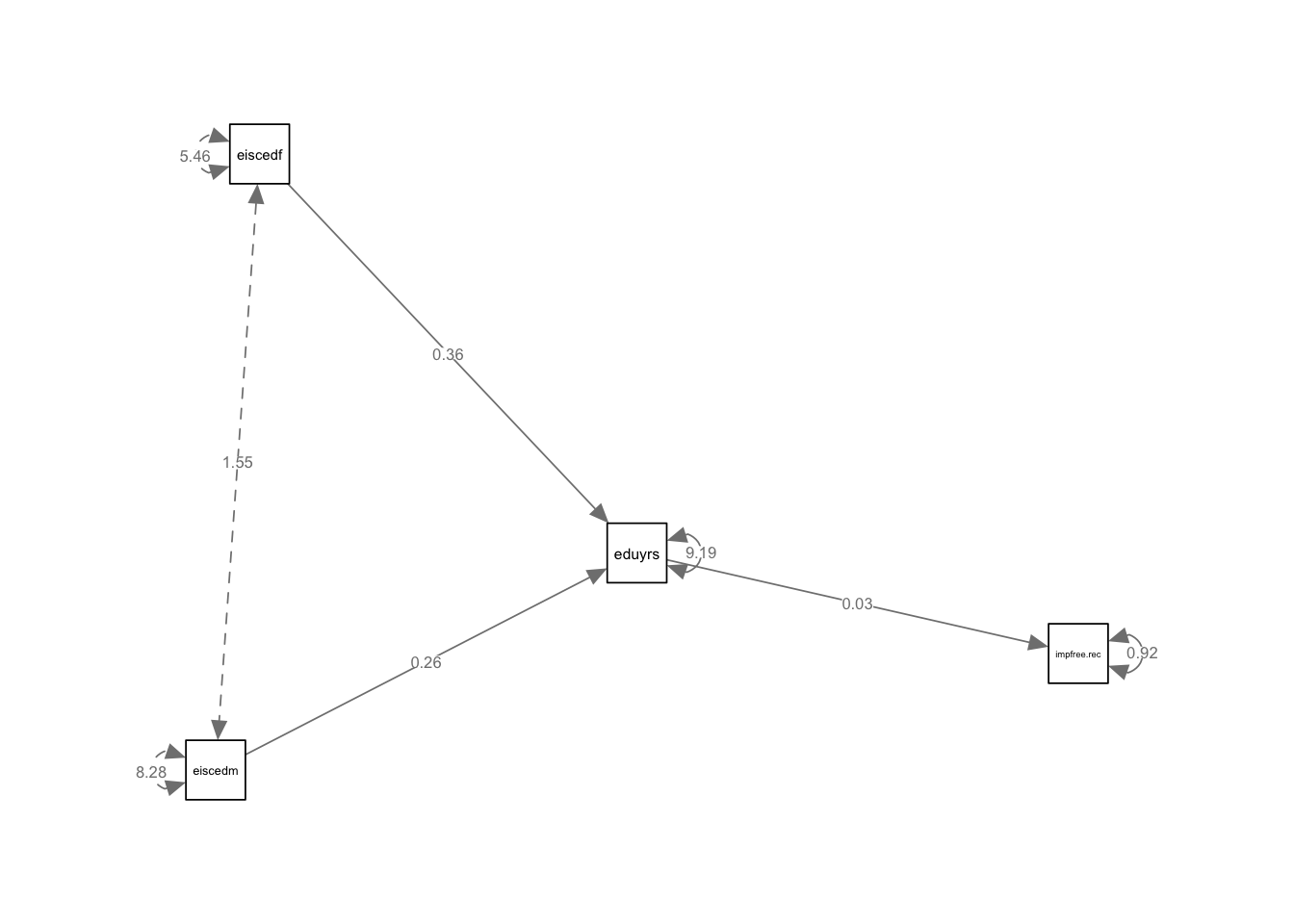
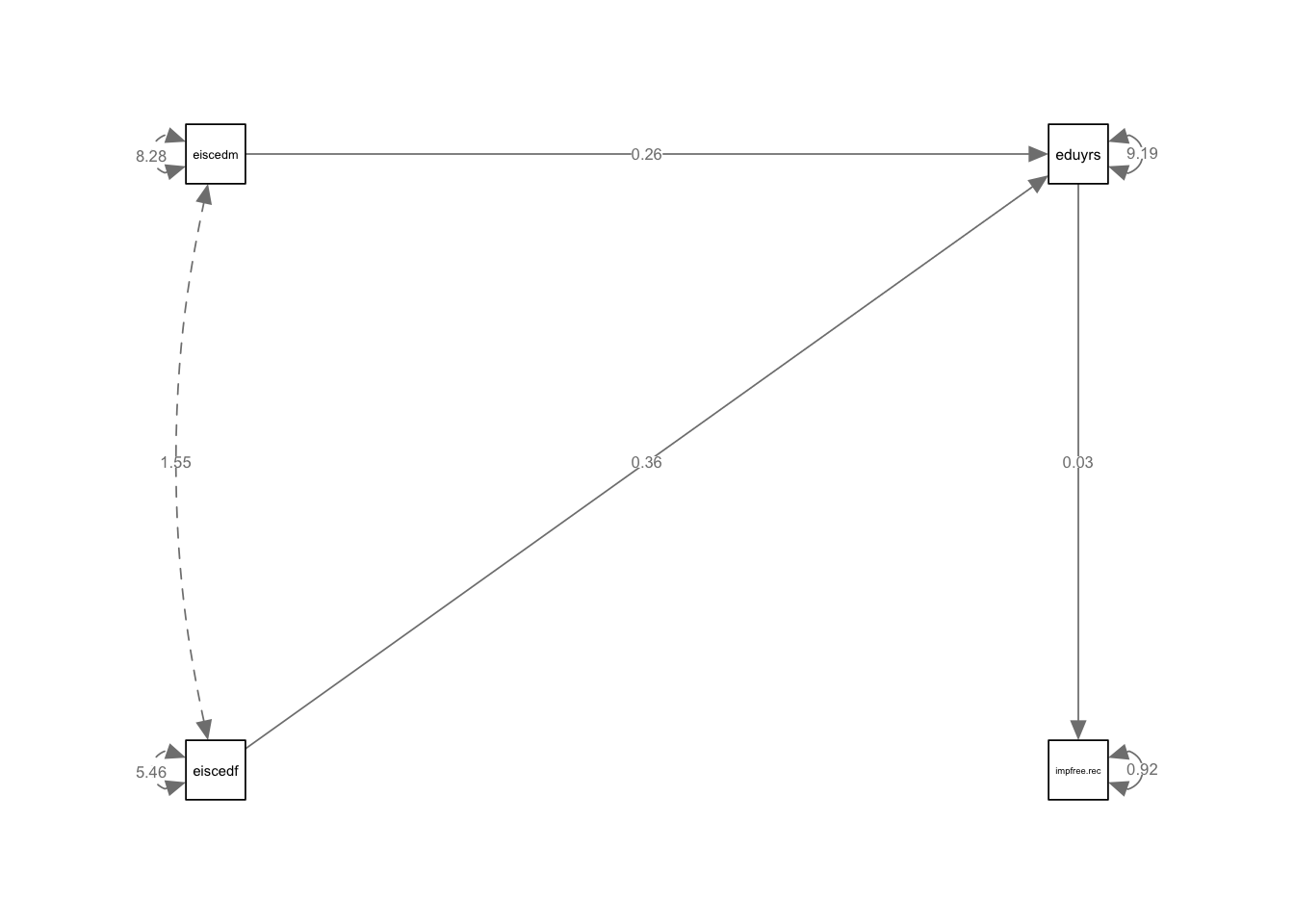
> .impfree.rec 0.918 0.032 29.103 0.0001.4 Диаграмма
Функция semPaths из пакета semPlot.
layout = "tree"
# функция из пакета semPlot
semPaths(path1,
layout = "tree", # логика расположения элементов
rotation = 2, # поворот логики расположения
nCharNodes = 0, # насколько можно сократить названия переменных?
whatLabels = "est" # какие значения отражать на графике
) 
1.5 Задание
- Постройте диаграмму в помощью пакета
semPlot; - Добавьте аргумент
col = "red", чтобы поменять цвет прямоугольников; - Добавьте аргументы
node.widthиnode.height, чтобы увеличить прямоугольники (значения по умолчанию =1)
1.6 Альтернативный вариант
library(LittleHelpers) # Установка - remotes::install_github("maksimrudnev/LittleHelpers")
lav_to_graph(path1)
1.7 Рассмотрим статистику согласия хи-квадрат
> lavaan 0.6-9 ended normally after 15 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 5
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 4.665
> Degrees of freedom 2
> P-value (Chi-square) 0.097Критерий хи-квадрат (Minimum Function Test Statistic) показывает отличие матрицы предсказанной моделью от матрицы данных (предсказанной истинной моделью). Если значимость этого критерия близка к нулю (p меньше порогового 0,05 или 0,01), то модель не подходит к данным.
Model test baseline model - другой хи-квадрат! Проверяет гипотезу о независимости переменных в модели, близкая к нулю значимость критерия говорит о наличии связи между переменными.
Значения всех параметров находятся в разделе Parameter estimates.
1.8 Рассмотрим полученные параметры модели
Только если статистики согласия удовлетворительны.
> lavaan 0.6-9 ended normally after 15 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 5
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 4.665
> Degrees of freedom 2
> P-value (Chi-square) 0.097
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> impfree.rec ~
> eduyrs 0.034 0.007 4.716 0.000
> eduyrs ~
> eiscedf 0.362 0.032 11.192 0.000
> eiscedm 0.255 0.026 9.704 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .impfree.rec 0.921 0.032 29.103 0.000
> .eduyrs 9.186 0.316 29.103 0.0001.9 lavaan
~ прямой эффект := непрямой эффект
Это не меняет саму модель, а только заставляет R вычислить дополнительные параметры (которые являются простой комбинацией существующих).
1.10 Модель 1 с дополнительными параметрами
path1 <- sem('
# Параметр влияния образования на ценность назвали «ED»
impfree.rec ~ ED*eduyrs
# Аналогично добавили названия параметров
eduyrs ~ ED_ED_F*eiscedf + ED_ED_M*eiscedm
# Непрямой эффект образования матери
indirect_M_ED := ED_ED_M * ED
',
data = Austria)
summary(path1)> lavaan 0.6-9 ended normally after 15 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 5
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 4.665
> Degrees of freedom 2
> P-value (Chi-square) 0.097
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> impfree.rec ~
> edyr (ED) 0.034 0.007 4.716 0.000
> eduyrs ~
> escd (ED_ED_F) 0.362 0.032 11.192 0.000
> escd (ED_ED_M) 0.255 0.026 9.704 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .impfree.rec 0.921 0.032 29.103 0.000
> .eduyrs 9.186 0.316 29.103 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> indirect_M_ED 0.009 0.002 4.242 0.0001.11 Задание
- Добавьте определение непрямого эффекта образования отца и посмотрите на результат.
- Значим ли непрямой эффект образования отца?
1.12 Модификации и альтернативные гипотезы
Основную гипотезу пока нельзя считать подтвержденной! Высокое согласие модели с данными еще не говорит о том, что альтернативная модель не будет согласована с ними еще лучше. Это важный принцип в путевом анализе. Окончательный вывод можно сделать только сравнив между собой несколько моделей.
Для того, чтобы сформировать альтернативную модель, сформулируем альтернативные гипотезы:
- Образование матери оказывает и прямое, и непрямое влияние на ценности свободы (гипотеза частичной медиации)
- Образование отца оказывает и прямое, и непрямое влияние на ценности свободы (гипотеза частичной медиации)
- Прямые эффекты образования отца и матери одинаковы.
Построим три новые модели для каждой альтернативной гипотезы и сравним их с исходной моделью.
1.13 Модель 2
Проверим гипотезу 1:
Образование матери оказывает и прямое, и непрямое влияние на ценности свободы (гипотеза частичной медиации)
- Добавьте прямой эффект образования матери на ценность свободы и назовите его “ED_M”.
- Вычислите общий (total) эффект образования матери на ценности свободы сложив прямой и непрямой эффект.
- После этого снова запустите модель и посмотрите на результаты через
summary. К предыдущим результатам должны были добавиться оценки прямого и общего эффектов. - Улучшилось ли качество модели в соответствии с хи-квадратом (он уменьшился?). Сравните модели функцией
lavTestLRT().
path2 <- sem('
impfree.rec ~ ED*eduyrs + ED_M*eiscedm
# Аналогично добавили названия парамтров
eduyrs ~ ED_ED_F*eiscedf + ED_ED_M*eiscedm
# Непрямой эффект образования матери
indirect_M_ED := ED_ED_M * ED
# Непрямой эффект образования отца
indirect_F_ED := ED_ED_F * ED
',
data = Austria)
lavTestLRT(path1, path2)1.14 Модель 3
Проверим гипотезу 2:
Образование отца оказывает и прямое, и непрямое влияние на ценности свободы (гипотеза частичной медиации)
- В исходную модель добавьте прямой эффект образования отца на ценность свободы и назовите его “ED_F”.
- Вычислите общий (total) эффект образования отца на ценности свободы сложив прямой и непрямой эффекты.
- Посмотрите на результаты через
summary(). К предыдущим результатам должны были добавиться оценки прямого и общего эффектов образования отца. - Улучшилось ли качество модели в соответствии с хи-квадратом и разницей хи-квадратов (LRT)?
- Чему в этой модели равен общий эффект образования матери?
path3 <- sem('
# прямые эффекты
impfree.rec ~ ED*eduyrs + ED_F*eiscedf
# эффекты образования родителей на образование респондента
eduyrs ~ ED_ED_F*eiscedf + ED_ED_M*eiscedm
# Непрямой эффект образования отца
indirect_F_ED := ED_ED_F * ED
# Общий эффект образования отца на
# ценность (то есть сумма прямого и непрямого эффектов)
total_F_ED := ED_ED_F * ED + ED_F
# Непрямой эффект образования матери
indirect_M_ED := ED_ED_M * ED
',
data = Austria)
summary(path3)> lavaan 0.6-9 ended normally after 17 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 6
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 4.461
> Degrees of freedom 1
> P-value (Chi-square) 0.035
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> impfree.rec ~
> edyr (ED) 0.033 0.007 4.343 0.000
> escd (ED_F) 0.005 0.010 0.451 0.652
> eduyrs ~
> escd (ED_ED_F) 0.362 0.032 11.192 0.000
> escd (ED_ED_M) 0.255 0.026 9.704 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .impfree.rec 0.921 0.032 29.103 0.000
> .eduyrs 9.186 0.316 29.103 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> indirect_F_ED 0.012 0.003 4.049 0.000
> total_F_ED 0.017 0.010 1.645 0.100
> indirect_M_ED 0.008 0.002 3.964 0.0001.15 Модель 4
Проверим дополнительную гипотезу 3
Прямые эффекты образования отца и матери одинаковы.
- Добавим прямые эффекты образования отца и матери на ценность свободы.
- В следующей модели, дополним их выражением равенства этих двух эффектов.
- Улучшилось ли качество модели? Являются ли эти модели вложенными – можно ли их сравнивать разницей хи-квадратов?
path4a <- sem('
# прямые эффекты
impfree.rec ~ ED*eduyrs + ED_M*eiscedm + ED_F*eiscedf
# эффекты образования родителей на образование респондента
eduyrs ~ ED_ED_F*eiscedf + ED_ED_M*eiscedm
ED_M == ED_F
',
data = Austria)
path4b <- sem('
# прямые эффекты
impfree.rec ~ ED*eduyrs + ED_M*eiscedm + ED_F*eiscedf
# эффекты образования родителей на образование респондента
eduyrs ~ ED_ED_F*eiscedf + ED_ED_M*eiscedm
',
data = Austria)
summary(path4a)> lavaan 0.6-9 ended normally after 18 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 7
> Number of equality constraints 1
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 1.325
> Degrees of freedom 1
> P-value (Chi-square) 0.250
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> impfree.rec ~
> edyr (ED) 0.028 0.008 3.688 0.000
> escd (ED_M) 0.011 0.006 1.828 0.067
> escd (ED_F) 0.011 0.006 1.828 0.067
> eduyrs ~
> escd (ED_ED_F) 0.362 0.032 11.192 0.000
> escd (ED_ED_M) 0.255 0.026 9.704 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .impfree.rec 0.919 0.032 29.103 0.000
> .eduyrs 9.186 0.316 29.103 0.000
>
> Constraints:
> |Slack|
> ED_M - (ED_F) 0.000> lavaan 0.6-9 ended normally after 17 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 7
>
> Used Total
> Number of observations 1694 1795
>
> Model Test User Model:
>
> Test statistic 0.000
> Degrees of freedom 0
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> impfree.rec ~
> edyr (ED) 0.029 0.008 3.748 0.000
> escd (ED_M) 0.018 0.009 2.113 0.035
> escd (ED_F) 0.001 0.011 0.115 0.909
> eduyrs ~
> escd (ED_ED_F) 0.362 0.032 11.192 0.000
> escd (ED_ED_M) 0.255 0.026 9.704 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .impfree.rec 0.918 0.032 29.103 0.000
> .eduyrs 9.186 0.316 29.103 0.0001.16 Постройте таблицу с оценкам параметров модели и диаграммы
Используйте функцию semTable() из одноименного пакета.
library("semTable")
library("htmltools")
final.tab <- semTable(
list("model 1"=path1,
"model 2" = path2,
"model 3" = path3),
columns = "estsestars",
type = "html",
print.results = FALSE
)| model 1 | model 2 | model 3 | |
| Estimate(Std.Err.) | Estimate(Std.Err.) | Estimate(Std.Err.) | |
| Regression Slopes | |||
| impfree.rec | |||
| eduyrs | 0.03(0.01)*** | 0.03(0.01)*** | 0.03(0.01)*** |
| eiscedm | 0.02(0.01)* | ||
| eiscedf | 0.00(0.01) | ||
| eduyrs | |||
| eiscedf | 0.36(0.03)*** | 0.36(0.03)*** | 0.36(0.03)*** |
| eiscedm | 0.26(0.03)*** | 0.26(0.03)*** | 0.26(0.03)*** |
| Residual Variances | |||
| impfree.rec | 0.92(0.03)*** | 0.92(0.03)*** | 0.92(0.03)*** |
| eduyrs | 9.19(0.32)*** | 9.19(0.32)*** | 9.19(0.32)*** |
| eiscedf | 5.46+ | 5.46+ | 5.46+ |
| eiscedm | 8.28+ | 8.28+ | 8.28+ |
| Residual Covariances | |||
| eiscedf w/eiscedm | 1.55+ | 1.55+ | |
| eiscedm w/eiscedf | 1.55+ | ||
| Constructed | |||
| indirect.M.ED | 0.01(0.00)*** | 0.01(0.00)*** | 0.01(0.00)*** |
| indirect.F.ED | 0.01(0.00)*** | 0.01(0.00)*** | |
| total.F.ED | 0.02(0.01) | ||
| Fit Indices | |||
| χ2 | 4.66(2) | 0.01(1) | 4.46(1)* |
| CFI | 0.99 | 1.00 | 0.99 |
| TLI | 0.98 | 1.02 | 0.94 |
| RMSEA | 0.03 | 0.00 | 0.05 |
| +Fixed parameter | |||
| *p<0.05, **p<0.01, ***p<0.001 | |||
1.17 Сравнение вложенных моделей
- Вложенные (nested) модели имеют один и то же набор наблюдаемых переменных, но различаются по количеству параметров.
- Редуцированная модель вложена в полную.
- Если убрать из любой модели один или несколько параметров, получится редуцированная модель, эти модели можно назвать вложенными.
- Если и убрать, и добавить параметры в модель с одними и теми же переменными, эти модели не будут вложенными.
- Невложенные модели можно сравнивать только по информационным критериям BIC и AIC.
1.17.1 Являются ли эти две модели вложенными?
1
2
3
4
5
6
7
1.18 Возможны ли эквавивалентные модели?
2 👉 Самостоятельное задание
Количество выпиваемого в неделю алкоголя (alcwkdy и alcwknd) среди австрийцев зависит от образования (eduyrs), возраста (agea), гендера (gndr), интенсивность социальной активности (sclact) и ценности гедонизма (impfun) – в Австрии.
Данные те же - 7 раунд ESS
2.1 Проверьте гипотезу 1
Г1. Влияние ценностей гедонизма на употребление алкоголя полностью опосредовано интенсивностью социальной активности.
При проверке учитывайте все релевантные (перечисленные выше) переменные.
Полная медиация подразумевает отсутствие прямого эффекта. Для проверки полной медиации нужно построить две модели и сравнить их между собой.
# Запускаем все необходимые библиотеки для данного семинара
library("lavaan")
library("foreign")
library("semPlot")
# Импортируем данные
ess7 <- read.spss("data/ESS7e02_1.sav",
use.value.labels = F,
use.missings = T,
to.data.frame = T)
# Отбираем австрийцев
Austria <- ess7[ess7$cntry == "AT",]
Austria$alc <- Austria$alcwkdy + Austria$alcwknd
#Austria$alc[Austria$alc==0] <- NA
Austria$alc.std <- scale(Austria$alc)
# Меняем кодировку для более удобной работы
Austria$impfun.rec <- 7 - Austria$impfun
Austria$gender <- factor(Austria$gndr, labels = c("Male", "Female") )
hist(Austria$alc)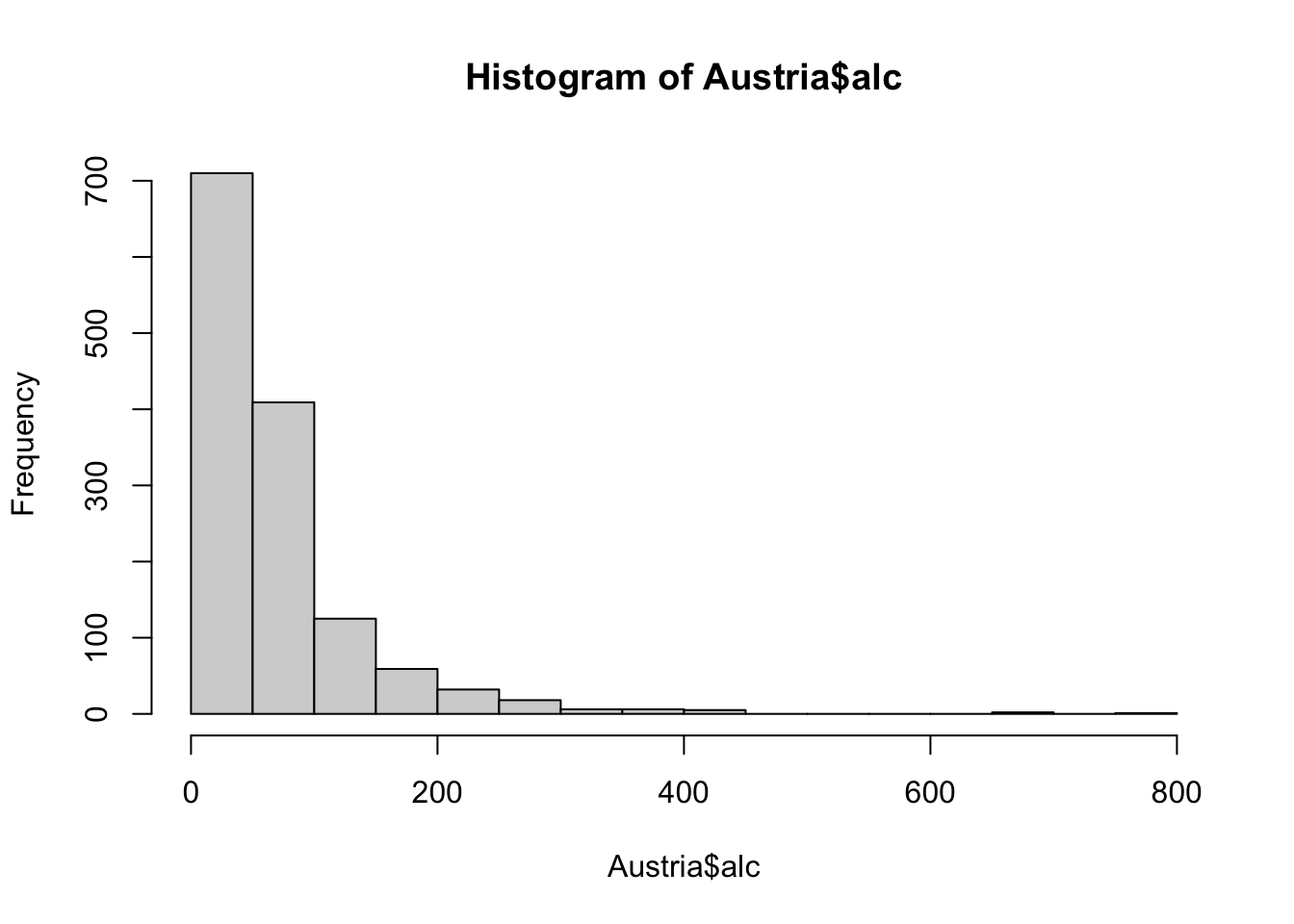
# собственно путевая модель
sem1a <- sem("alc ~ eduyrs + agea + gender + SOC*sclact + impfun.rec;
sclact ~ SOC_FUN*impfun.rec;
IND_SOC_FUN := SOC * SOC_FUN;
",
data = Austria)
sem1b <- sem("alc ~ eduyrs + agea + gender + SOC*sclact;
sclact ~ SOC_FUN*impfun.rec;
IND_SOC_FUN := SOC * SOC_FUN;
",
data = Austria)
summary(sem1a)> lavaan 0.6-9 ended normally after 65 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 8
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 3.170
> Degrees of freedom 3
> P-value (Chi-square) 0.366
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc ~
> eduyrs -0.817 0.573 -1.425 0.154
> agea -0.437 0.108 -4.057 0.000
> gender -33.796 3.659 -9.237 0.000
> sclact (SOC) 6.473 2.208 2.931 0.003
> impfn.r 3.161 1.714 1.844 0.065
> sclact ~
> impfn.r (SOC_) 0.146 0.020 7.235 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc 4515.561 173.355 26.048 0.000
> .sclact 0.682 0.026 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_SOC_FUN 0.943 0.347 2.717 0.007> lavaan 0.6-9 ended normally after 54 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 7
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 6.557
> Degrees of freedom 4
> P-value (Chi-square) 0.161
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc ~
> eduyrs -0.886 0.573 -1.546 0.122
> agea -0.483 0.105 -4.602 0.000
> gender -33.943 3.662 -9.269 0.000
> sclact (SOC) 7.268 2.172 3.347 0.001
> sclact ~
> impfn.r (SOC_) 0.146 0.020 7.235 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc 4526.845 173.788 26.048 0.000
> .sclact 0.682 0.026 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_SOC_FUN 1.059 0.348 3.037 0.002# Получается, что модели одинаково подходят к данным, выбираем более простую, т.е. без прямого эффекта ценностей гедонизма. Гипотеза 1 подтверждается.- Удовлетворительны ли статистики согласия?
- Значимы ли интересующие нас коэффициенты?
- Подтвердилась ли Гипотеза 1?
2.2 Проверьте гипотезу 2
Г2. Влияние возраста на употребление алкоголя частично опосредовано ценностью гедонизма.
Для проверки частичной медиации нужно построить модель с прямым и непрямым эффектом и оценить их значимость.
sem2.partial <- sem("alc ~ eduyrs + gndr + agea + SOC*sclact + FUN*impfun.rec;
# осталось от предыдушей модели
#sclact ~ SOC_FUN*impfun.rec;
#IND_SOC_FUN := SOC * SOC_FUN;
# проверка гипетезы 2
impfun.rec ~ FUN_AGE*agea;
IND_FUN_AGE := FUN_AGE * FUN;
",
data = Austria)
sem2.full <- sem("alc ~ eduyrs + gender + SOC*sclact + FUN*impfun.rec;
# осталось от предыдушей модели - частичная медиации
sclact ~ SOC_FUN*impfun.rec;
IND_SOC_FUN := SOC * SOC_FUN;
# проверка гипотезы 2
impfun.rec ~ FUN_AGE*agea;
IND_FUN_AGE := FUN_AGE * FUN;
",
data = Austria)
summary(sem2.partial)> lavaan 0.6-9 ended normally after 67 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 8
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 58.154
> Degrees of freedom 3
> P-value (Chi-square) 0.000
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc ~
> eduyrs -0.817 0.573 -1.427 0.154
> gndr -33.796 3.658 -9.239 0.000
> agea -0.437 0.107 -4.067 0.000
> sclact (SOC) 6.473 2.168 2.985 0.003
> impfn.r (FUN) 3.161 1.680 1.881 0.060
> impfun.rec ~
> agea (FUN_) -0.014 0.002 -8.478 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc 4515.560 173.355 26.048 0.000
> .impfun.rec 1.179 0.045 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_FUN_AGE -0.045 0.024 -1.837 0.066> lavaan 0.6-9 ended normally after 65 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 9
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 24.917
> Degrees of freedom 6
> P-value (Chi-square) 0.000
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc ~
> eduyrs -0.418 0.569 -0.735 0.463
> gender -32.962 3.675 -8.970 0.000
> sclact (SOC) 6.193 2.222 2.787 0.005
> impfn.r (FUN) 4.783 1.680 2.847 0.004
> sclact ~
> impfn.r (SOC_) 0.146 0.020 7.235 0.000
> impfun.rec ~
> agea (FUN_) -0.014 0.002 -8.478 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc 4570.284 175.456 26.048 0.000
> .sclact 0.682 0.026 26.048 0.000
> .impfun.rec 1.179 0.045 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_SOC_FUN 0.902 0.347 2.601 0.009
> IND_FUN_AGE -0.068 0.025 -2.699 0.007# Получается, что модель с прямым эффектом возраста лучше подходит к данным, а непрямой эффект является незначимым. Отвергаем гипотезу в пользу полного отсутствия медиации (ни полной, ни частичной не обнаружено).- Удовлетворительны ли статистики согласия?
- Значимы ли интересующие нас коэффициенты?
- Подтвердилась ли Гипотеза 2?
- Каковы возможные прямые эффекты?
- Какие непрямые эффекты тут возможны?
2.3 Проверьте гипотезу 3
Г3. Влияние возраста на употребление алкоголя опосредовано уровнем образования, эффект которого в свою очередь опосредован социальной активностью (гипотеза последовательной медиации).
Эффект последовательной медиации вычисляется так же как и для парной - умножением коэффициентов в цепочке, ведущей от возраста к алкоголю.
# в этой модели удален прямой эффект impfun.rec, т.к. был отвергнут при проверке гипотезы 1
sem3 <- sem("alc.std ~ eduyrs + gender + agea + SOC*sclact;
# осталось от проверки гип1
sclact ~ SOC_FUN*impfun.rec;
IND_SOC_FUN := SOC * SOC_FUN;
# осталось от проверки гип2
impfun.rec ~ FUN_AGE*agea;
# проверка гипотезы 3
eduyrs ~ EDU_AGE*agea;
sclact ~ SOC_EDU*eduyrs;
ind__age := SOC * SOC_EDU * EDU_AGE ;
",
data = Austria)
summary(sem3)> lavaan 0.6-9 ended normally after 33 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 12
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 10.437
> Degrees of freedom 6
> P-value (Chi-square) 0.107
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc.std ~
> eduyrs -0.013 0.008 -1.545 0.122
> gender -0.485 0.052 -9.269 0.000
> agea -0.007 0.002 -4.602 0.000
> sclact (SOC) 0.104 0.031 3.345 0.001
> sclact ~
> impfn. (SOC_F) 0.146 0.020 7.261 0.000
> impfun.rec ~
> agea (FUN_) -0.014 0.002 -8.478 0.000
> eduyrs ~
> agea (EDU_) -0.029 0.005 -6.012 0.000
> sclact ~
> eduyrs (SOC_E) 0.009 0.007 1.317 0.188
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc.std 0.924 0.035 26.048 0.000
> .sclact 0.681 0.026 26.048 0.000
> .impfun.rec 1.179 0.045 26.048 0.000
> .eduyrs 10.162 0.390 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_SOC_FUN 0.015 0.005 3.038 0.002
> ind__age -0.000 0.000 -1.201 0.230- Удовлетворительны ли статистики согласия?
- Значимы ли интересующие нас коэффициенты?
- Подтвердилась ли Гипотеза 3?
2.4 Какие еще гипотезы возможны?
- Какие еще прямые эффекты тут возможны ?
- Какие непрямые эффекты тут возможны?
Сформулируйте гипотезы и ответьте на вопросы:
- Какие из переменных в модели являются эндогенными, а какие экзогенными?
- Сколько параметров в этой модели?
- Сколько уникальных дисперсий и ковариаций?
- Сколько степеней свободы?
- Идентифицирована ли эта модель?
- Это модель полной или частичной медиации?
- Все ли гипотезы проходят четыре условия каузальности?
2.5 Модификационные индексы
Рассмотрите модификационные индексы, которые послужат подсказками для ре-спецификации модели (Показывает насколько уменьшится хи-квадрат модели при добавлении какой-либо взаимосвязи). Для вывода значений модификационных индексов можно воспользоваться функцией modindices().
Обратите внимание, что не все из них имеют содержательный смысл.
- Какие параметры следует добавить в модель, если слепо верить модификационным индексам? Добавьте этот параметр в модель и сравните с исходной моделью - улучшилось ли качество?
2.6 Моделирование
- Постройте модели, которые могут проверить вашу гипотезу.
- Сравните модели между собой (сравнивать можно только вложенные!)
- Сделайте вывод по каждой из гипотез.
sem3.modified <- sem("alc.std ~ eduyrs + gender + agea + SOC*sclact;
# осталось от проверки гип1
sclact ~ SOC_FUN*impfun.rec;
IND_SOC_FUN := SOC * SOC_FUN;
# осталось от проверки гип2
impfun.rec ~ FUN_AGE*agea;
# проверка гипотезы 3
eduyrs ~ EDU_AGE*agea;
sclact ~ SOC_EDU*eduyrs;
ind__age := SOC * SOC_EDU * EDU_AGE ;
# новая строчка на основании мод.индексов
impfun.rec ~ eduyrs;
",
data = Austria)
summary(sem3.modified)> lavaan 0.6-9 ended normally after 34 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 13
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 5.797
> Degrees of freedom 5
> P-value (Chi-square) 0.326
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc.std ~
> eduyrs -0.013 0.008 -1.546 0.122
> gender -0.485 0.052 -9.269 0.000
> agea -0.007 0.002 -4.602 0.000
> sclact (SOC) 0.104 0.031 3.345 0.001
> sclact ~
> impfn. (SOC_F) 0.146 0.020 7.265 0.000
> impfun.rec ~
> agea (FUN_) -0.015 0.002 -8.729 0.000
> eduyrs ~
> agea (EDU_) -0.029 0.005 -6.012 0.000
> sclact ~
> eduyrs (SOC_E) 0.009 0.007 1.318 0.187
> impfun.rec ~
> eduyrs -0.020 0.009 -2.156 0.031
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc.std 0.924 0.035 26.048 0.000
> .sclact 0.681 0.026 26.048 0.000
> .impfun.rec 1.175 0.045 26.048 0.000
> .eduyrs 10.162 0.390 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_SOC_FUN 0.015 0.005 3.038 0.002
> ind__age -0.000 0.000 -1.202 0.230# индексы предлагают вернуть прямой эффект impfun.rec, можем это сделать, но лучше не делать. В целом, на этом модель можно считать итоговой, т.к. более не осталось осмысленных мод.индексов и содержательных гипотез, а хи-кв модели приблизился к идеальному.
sem3.modified2 <- sem("alc.std ~ eduyrs + gender + agea + SOC*sclact + impfun.rec;
# осталось от проверки гип1
sclact ~ SOC_FUN*impfun.rec;
IND_SOC_FUN := SOC * SOC_FUN;
# осталось от проверки гип2
impfun.rec ~ FUN_AGE*agea;
# проверка гипотезы 3
eduyrs ~ EDU_AGE*agea;
sclact ~ SOC_EDU*eduyrs;
ind__age := SOC * SOC_EDU * EDU_AGE ;
# новая строчка на основании мод.индексов
impfun.rec ~ eduyrs;
",
data = Austria)
summary(sem3.modified2)> lavaan 0.6-9 ended normally after 34 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 14
>
> Used Total
> Number of observations 1357 1795
>
> Model Test User Model:
>
> Test statistic 2.410
> Degrees of freedom 4
> P-value (Chi-square) 0.661
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Regressions:
> Estimate Std.Err z-value P(>|z|)
> alc.std ~
> eduyrs -0.012 0.008 -1.424 0.154
> gender -0.483 0.052 -9.241 0.000
> agea -0.006 0.002 -4.059 0.000
> sclact (SOC) 0.092 0.032 2.929 0.003
> impfn. 0.045 0.024 1.844 0.065
> sclact ~
> impfn. (SOC_F) 0.146 0.020 7.265 0.000
> impfun.rec ~
> agea (FUN_) -0.015 0.002 -8.729 0.000
> eduyrs ~
> agea (EDU_) -0.029 0.005 -6.012 0.000
> sclact ~
> eduyrs (SOC_E) 0.009 0.007 1.318 0.187
> impfun.rec ~
> eduyrs -0.020 0.009 -2.156 0.031
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .alc.std 0.922 0.035 26.048 0.000
> .sclact 0.681 0.026 26.048 0.000
> .impfun.rec 1.175 0.045 26.048 0.000
> .eduyrs 10.162 0.390 26.048 0.000
>
> Defined Parameters:
> Estimate Std.Err z-value P(>|z|)
> IND_SOC_FUN 0.014 0.005 2.717 0.007
> ind__age -0.000 0.000 -1.179 0.2392.7 Возможны ли эквавивалентные модели?
2.8 Постройте диаграмму двух лучших моделей
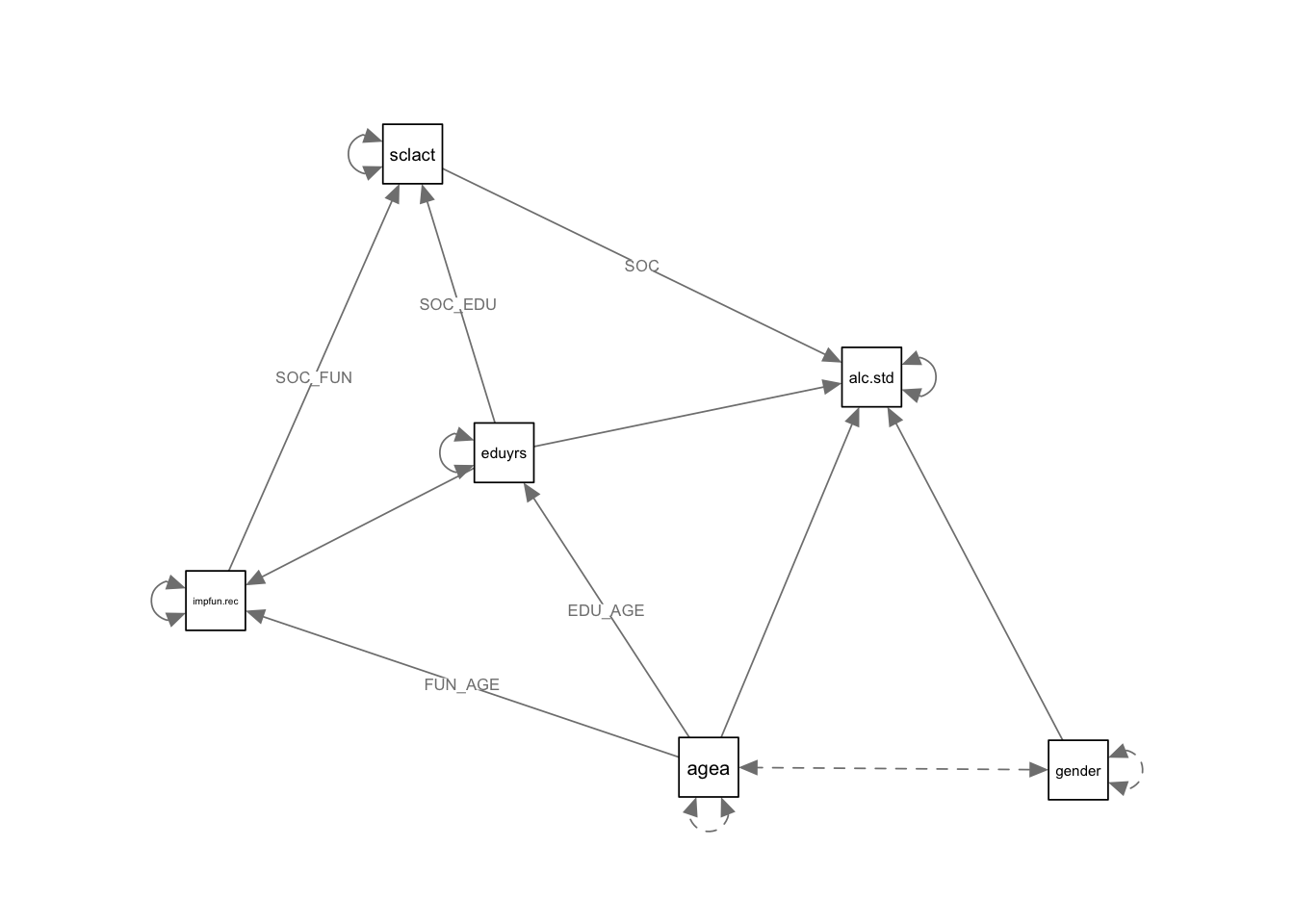
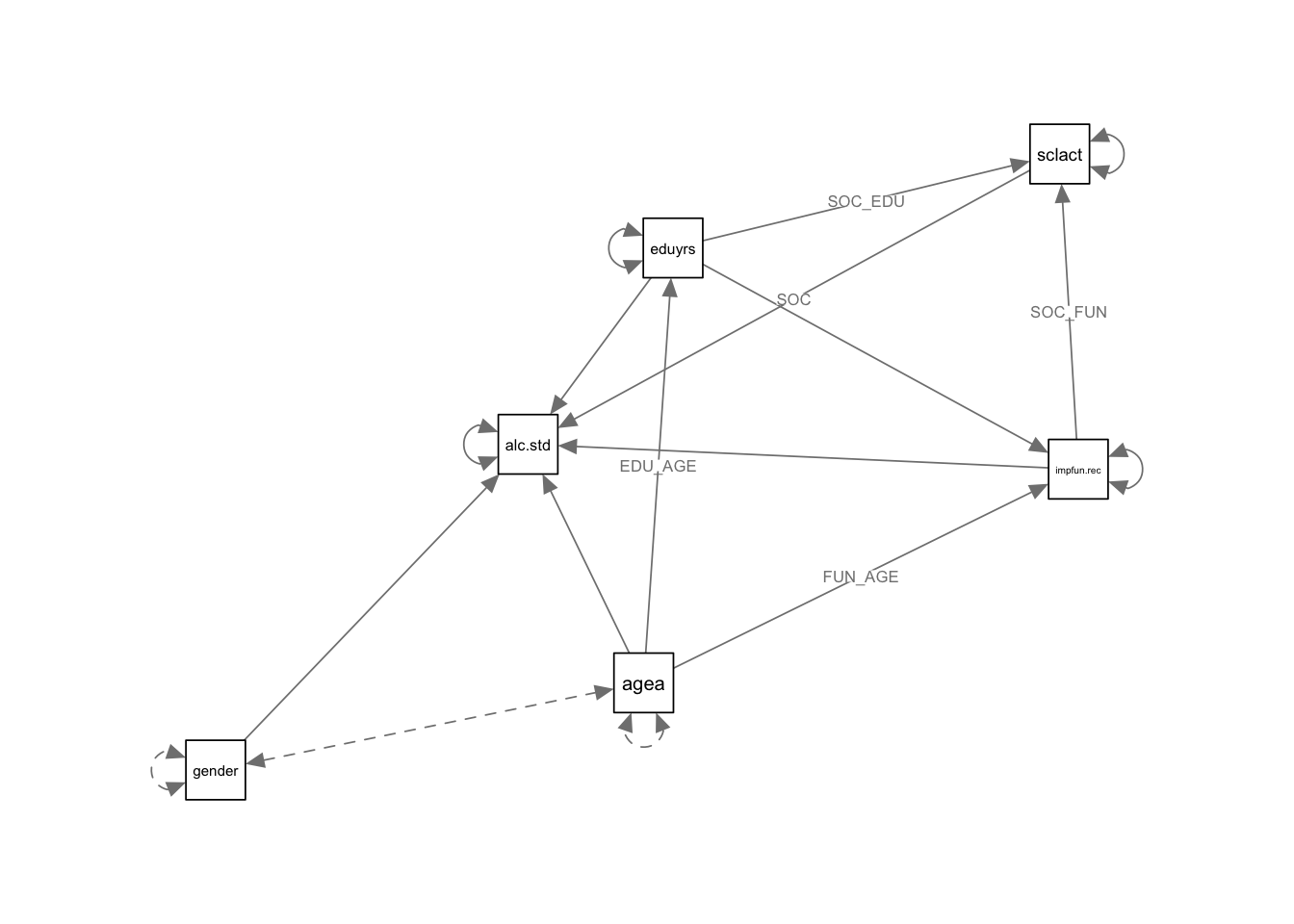
2.9 Оформите две лучшие модели в таблицы
library("semTable")
library("htmltools")
stab1 <- semTable(
list("model 1"=sem3,
"model 2" = sem3.modified,
"model 3" = sem3.modified2),
columns = "estsestars",
type = "html",
print.results = FALSE
)| model 1 | model 2 | model 3 | |
| Estimate(Std.Err.) | Estimate(Std.Err.) | Estimate(Std.Err.) | |
| Regression Slopes | |||
| alc.std | |||
| eduyrs | -0.01(0.01) | -0.01(0.01) | -0.01(0.01) |
| gender | -0.48(0.05)*** | -0.48(0.05)*** | -0.48(0.05)*** |
| agea | -0.01(0.00)*** | -0.01(0.00)*** | -0.01(0.00)*** |
| sclact | 0.10(0.03)*** | 0.10(0.03)*** | 0.09(0.03)** |
| impfun.rec | 0.05(0.02) | ||
| sclact | |||
| impfun.rec | 0.15(0.02)*** | 0.15(0.02)*** | 0.15(0.02)*** |
| eduyrs | 0.01(0.01) | 0.01(0.01) | 0.01(0.01) |
| impfun.rec | |||
| agea | -0.01(0.00)*** | -0.01(0.00)*** | -0.01(0.00)*** |
| eduyrs | -0.02(0.01)* | -0.02(0.01)* | |
| eduyrs | |||
| agea | -0.03(0.00)*** | -0.03(0.00)*** | -0.03(0.00)*** |
| Residual Variances | |||
| alc.std | 0.92(0.04)*** | 0.92(0.04)*** | 0.92(0.04)*** |
| sclact | 0.68(0.03)*** | 0.68(0.03)*** | 0.68(0.03)*** |
| impfun.rec | 1.18(0.05)*** | 1.17(0.05)*** | 1.17(0.05)*** |
| eduyrs | 10.16(0.39)*** | 10.16(0.39)*** | 10.16(0.39)*** |
| gender | 0.25+ | 0.25+ | 0.25+ |
| agea | 311.94+ | 311.94+ | 311.94+ |
| Residual Covariances | |||
| gender w/agea | -0.45+ | -0.45+ | -0.45+ |
| Constructed | |||
| IND.SOC.FUN | 0.02(0.00)** | 0.02(0.00)** | 0.01(0.00)** |
| ind..age | -0.00(0.00) | -0.00(0.00) | -0.00(0.00) |
| Fit Indices | |||
| χ2 | 10.44(6) | 5.80(5) | 2.41(4) |
| CFI | 0.98 | 1.00 | 1.00 |
| TLI | 0.96 | 0.99 | 1.02 |
| RMSEA | 0.02 | 0.01 | 0.00 |
| +Fixed parameter | |||
| *p<0.05, **p<0.01, ***p<0.001 | |||
2.10 Bonus
Сформулируйте гипотезу и постройте соответствующую модель с двумя синхронными медиаторами.