🚗 Модель и моделирование

Модель

Описание, аналогия
Уменьшенная копия чего-либо
Набор идей и чисел, который описывает прошлое, настоящее или будущее состояние вещей (таких как экономика или бизнес)
Система постулатов, данных и выводов, представленных в виде математического описания сущности или состояния вещей

Параметры модели

Параметр − характеристика или свойство, позволяющее определить некую систему.
Параметры модели – все неизвестные, искомые части модели.
Результат наложения модели на эмпирические данные.

* Параметры ≠ переменные! Наблюдаемые переменные − часть данных, параметры − часть модели.

Правило экономичности (parsimony)

Бóльшее число параметров автоматически повышает способность модели объяснять данные, но снижает ее способность объяснить процессы в генеральной совокупности;

Правило экономичности (оно же Бритва Оккама  ): чем проще модель, тем лучше. Идеал − минимальное количество параметров при максимальном качестве модели.

~~Если две модели имеют одинаковое согласие с данными, предпочтение следует отдавать более простой модели.~~

Количество степеней свободы (degrees of freedom, df) − число заранее известных параметров, которое потенциально позволяет найти значения неизвестных параметров. Величина, обратная количеству параметров. Большее число степеней свободы указывает на более экономичную модель.

(Эмпирические) данные

Опыт, информация, получаемая органами чувств;
Фактическая информация, используемая в аргументации, дискуссии или вычислениях.

❗️Нужно четко разделять данные (имеющиеся, наблюдаемые, известные значения) и неизвестные.

Структура модели

вопрос, который мы задаем (гипотеза);
на неправильно поставленный вопрос невозможно получить правильный ответ
(неосознаваемые) части модели: “по умолчанию”, допущения;
линейность, причинно-следственые отношения, отсутствие ошибки измерения

❗️структура модели является частью данных, которые мы вводим в модель, но редко осознается как данные.

Подходы к разработке моделей

Конфирматорный (подтверждающий) подход
- требует большого количества информации о предмете исследования, используется для проверки очень конкретных теорий: результат бинарный, подтверждение или отвержение.
Альтернативные модели
- требует наличия не менее двух противоречащих друг другу содержательных теорий.
Генерирование моделей (model generation)
- используется при отсутствии теорий.

Выбор подхода зависит от степени разработанности теории и знания изучаемого предмета.

Проверка гипотез с помощью моделей требует знания языков

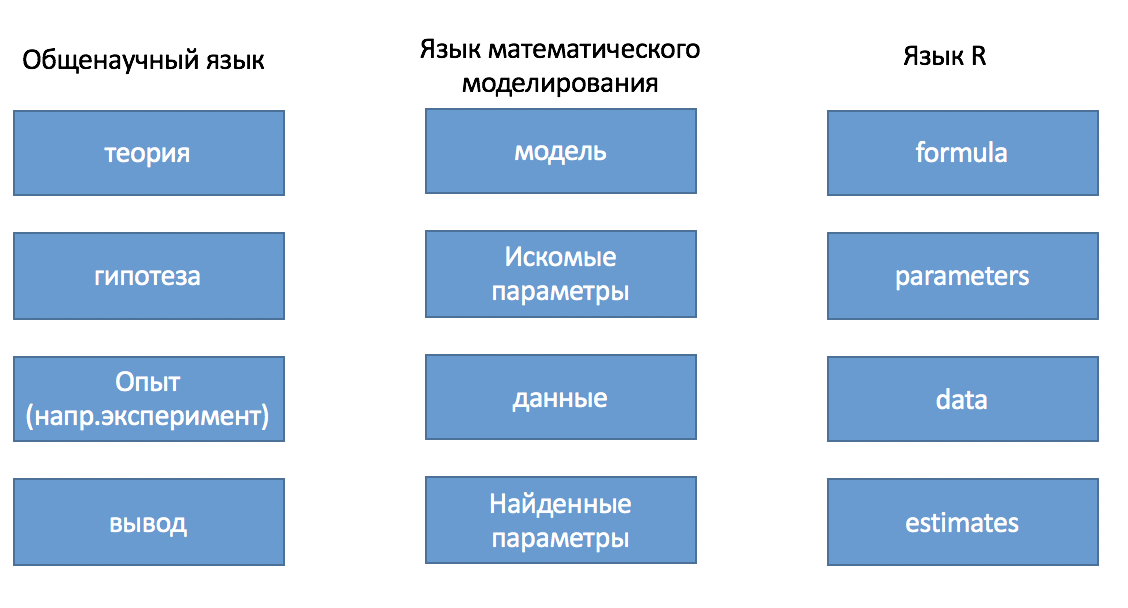
↔︎️ От регрессии − к путевому анализу

Парная линейная регрессия

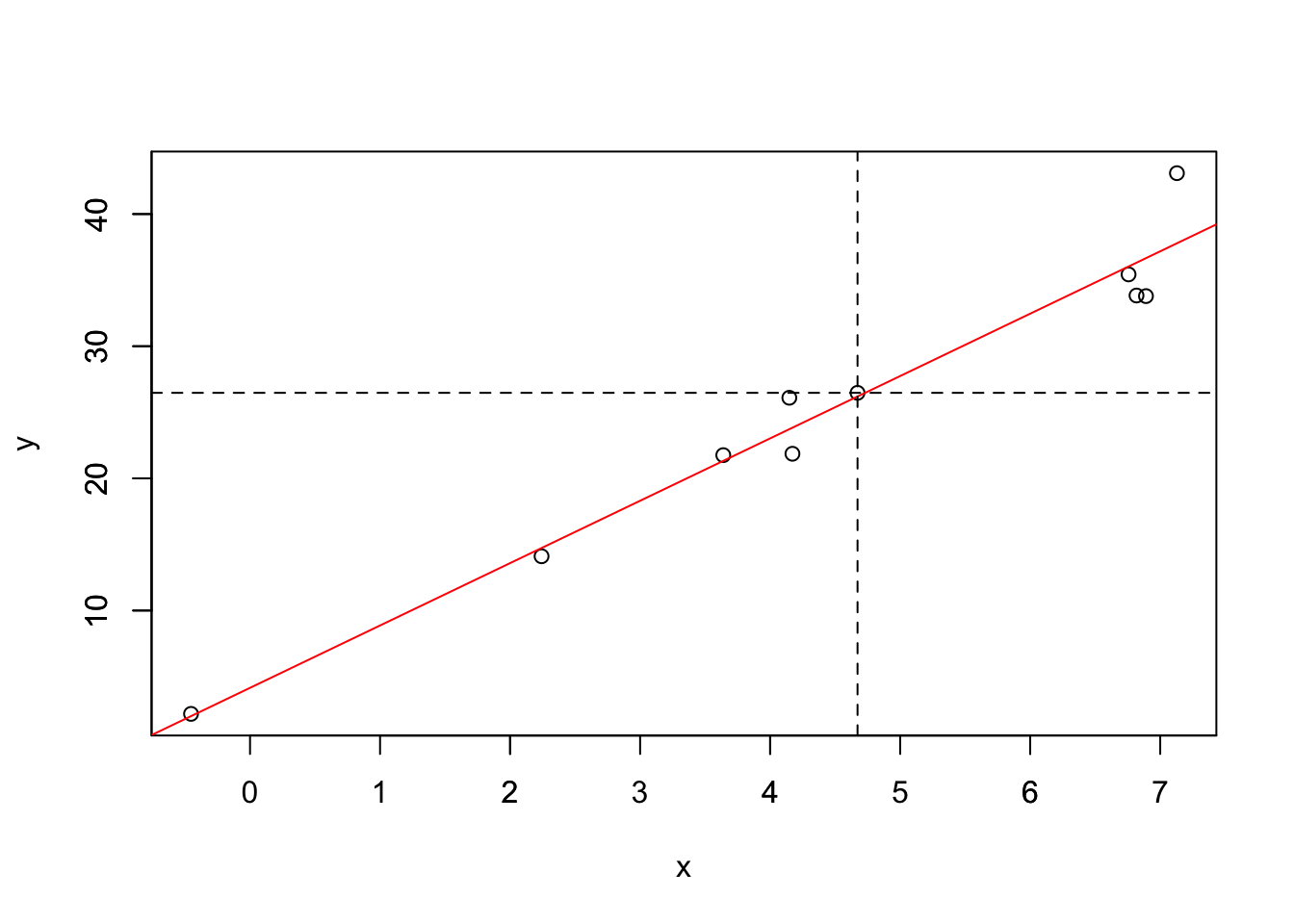
\[ y = a + bx + \epsilon, \]

\(a\)− константа/свободный член/интерсепт;
\(b\) − нестандартизованный регрессионный коэффициент;
\(\epsilon\) − дисперсия остатков.

Диаграмма

\[ y = a + bx + \epsilon\]

Условные обозначения в диаграммах

Nodes (узлы/вершины)

Edges (ребра)

~~Отсутствие стрелки~~ – связь считается равной нулю.

Множественная регрессия

\[ y = a + b_1x_1 + b_2x_2 + b_3x_3 + \epsilon \]

Путевой анализ

\[ y = b_1x_1 + b_2x_2 + b_3x_3 + \epsilon_y \] Отбросим константу (представим, что она равна нулю из-за того, что все переменные специальным образом стандартизированы).

В дополнение к одному уравнению появилось второе:

\[ x_2 = b_{x1 -> x2}x_1 + \epsilon_{x2} \]

Теперь подставим \(x_2\) в первое уравнение:

\[ y = b_1x_1 + b_2(b_{x1-> x2}x_1 + \epsilon_{x2}) + b_3x_3 + \epsilon_y \] или

\[ y = b_1x_1 + b_2b_{x1-> x2}x_1 + b_2\epsilon_{x2} + b_3x_3 + \epsilon_y \] Теперь разберемся что здесь к чему.

\(b_1\) − влияние \(x_1\) на \(y\)
\(b_2b_{x1->x2}\) − непрямое влияние \(x_1\) на \(y\), опосредованное \(x_2\)
\(b_2\epsilon_{x2}\) − остаток \(x_2\)
\(b_3\) − влияние \(x_3\) на \(y\)
\(\epsilon_y\) − остаток \(y\).

Непрямые эффекты

Непрямой эффект − произведение двух прямых в пути из точки \(x_1\) в точку \(y\) (поэтому путевой анализ).

Прямой эффект также тут существует.

Общий эффект – это сумма прямого и непрямого эффектов.

Когда в модели представлен и прямой, и непрямой эффект, она называется модель частичной медиации, а все опосредующие переменные (здесь это \(x_2\)) − медиаторами.

Модель полной медиации

Прямой эффект от x₁ к y отсутствует.

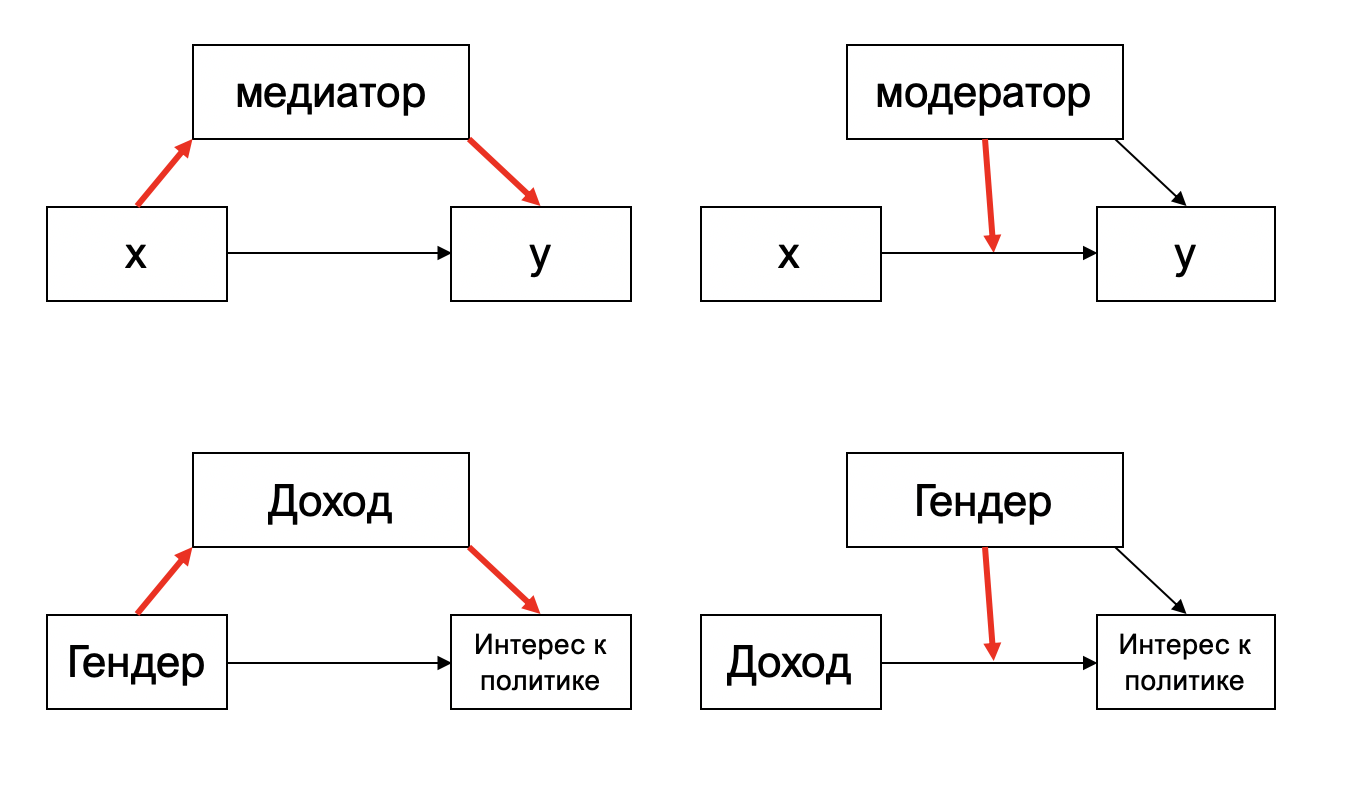
Медиатор и модератор

Медиатор – проводник, который «пропускает через себя» влияния одной переменной на другую. Выражается одной переменной, которая зависит от другой и влияет на третью.

Модератор – посредник, который усиливает или ослабляет эффект одной переменной на другую, лишь опосредованно участвует в причинно- следственных отношениях. Ср. «модератор в фокус-группе». Выражается через интеракцию (взаимодействие) двух или более переменных.

Эндогенные и экзогенные переменные

Поскольку в путевом анализе много зависимых переменных, некоторые из них также являются независимыми для других. Поэтому используется другая классификация:

Экзогенные переменные не имеют причин/предикторов в данной модели.
Эндогенные − все, которые имеют предикторы в данной модели.

Рекурсивные и нерекурсивные модели

В структурных уравнениях значения этих терминов перевернуты.

Нерекурсивными моделями называются модели с циклами (более сложные, касаться не будем). Рекурсивными - модели без циклов.

🆔 Идентификация модели

свойство структуры модели, обеспечивающей возможность нахождения уникальных значений параметров.

Пример неидентифицированной модели (две неизвестных, одно известное, df = -1):

\(x + y = 10\)

Пример идентифицированной модели (два известных, одно неизвестное, df = 1):

\(x + 1 = 10\)

Пример идентифицированной модели, параметры \(y\) и \(x\) зафиксированы равеными друг другу (одно неизвестное, одно известное, df = 0):

\(x + y = 10\)

Условия

Количество степеней свободы равно или больше нуля (df ≥ 0).

Рекурсивные путевые модели всегда идентифицированы.

Модели КФА сложнее идентифицировать (на следующей лекции).

Сколько тут параметров и степеней свободы?

Количество параметров: все прямые эффекты (4), остатки (2), дисперсии экзогенных переменных* (2) = 8.

* На путевой диаграмме не отображаются.

Количество “наблюдений” (уникальных элементов в матрице дисперсии-ковариации): \[ N_{obs} = {k*(k+1)} / 2, \\ где~k − количество~наблюдаемых~переменных.\\ N_{obs} = {4*(4+1)} / 2 = 10 \]

Число степеней свободы: Количество “наблюдений” минус Количество параметров. 10 − 8 = 2.

Это означает, что в модель теоретически можно добавить еще 2 параметра для ее точного определения.

Виды идентификации

Overidentified (переопределенные/идентифицированные) df >0
Just-identified (точно определенные/едва-идентифицированные) df=0 Всегда имеет высокие показатели согласия. Множественные регрессии.
Underidentified (недоопределенные/слабо идентифицированные)
- df<0
- df>0, но некоторые параметры все же не могут быть идентифицированы.

👌 Качество модели

Определяется по разному, но основной критерий − это ~~близость найденных параметров к истинным, то есть к существующим в генеральной совокупности~~.

Отличается от близости модели к данным.

Хи-квадрат модели

Хи-квадрат сравнивает дисперсии и ковариации, предсказанные моделью с эмпирическими (наблюдаемыми) матрицами ковариации.

Нулевая гипотеза – предсказанная матрица дисперсий-ковариаций равна матрице эмпирической, поэтому большие (и значимо отличающиеся от нуля) значения хи-квадрат указывают на плохое согласие модели с данными.

Больший хи-квадрат указывает на случайность возникновения матрицы ковариаций.

При высоких р-value (обычно больше 0,05) различия между предсказанной и эмпирической матрицей ковариации незначимы и модель считается ‘верной’.

В едва-идентифицированных моделях всегда χ2=0, но это ничего не значит.

Чувствителен (всегда значим) к большим выборкам (>1000)

\[\chi^2 = F_{max.lik.}(N-1) \] при количестве степеней свободы, которое есть у модели, F_max.lik. − значение функции наибольшего правдоподобия, N − размер выборки.

Вложенные модели и разница хи-квадратов

Вложенной (nested) моделью называется модель с одним или более пропущенными переменными/параметрами. Редуцированная модель вложена в полную. Вложенные модели имеют один и то же набор наблюдаемых переменных, но различаются по количеству параметров.

Разницу между вложенными моделями можно проверить, посмотрев насколько ухудшилось согласие модели при исключении одного или нескольких параметров:

Если разница хи-квадратов χ²_delta= χ²_reduced – χ²_full при df=df_reduced − df_full значима, то полная модель лучше объясняет данные, если незначима, то редуцированная и полная модели имеют одинаковое качество. Следуя правилу экономности, в последнем случае предпочтение отдается редуцированной модели.

Редуцированная

Полная

Модификационные индексы

Предварительная оценка параметров до включения их в модель.

MI – модификационный индекс (на сколько уменьшится хи-квадрат модели, если включить данный параметр)

EPC – expected parameter change – каково будет значение параметра если его включить в модель

Работают только для отдельных параметров и являются лишь приблизительными оценками, подсказками для ре-спецификации.

🧠 Причинно-следственные отношения

Мантра: “Correlation is not causation”

Предшествование во времени
Направление связи не является обратным (необходимо в связи с ошибкой ретроспективного измерения)
Взаимосвязь (ковариация)
Изолированность (никакая третья переменная не объясняет ковариацию)
Известная форма распределения (детерминистское, вероятностное)

1. Предшествование во времени

Чтобы проверить НАПРАВЛЕНИЕ причинности, в эксперименте есть возможность фиксировать время событий. Более раннее событие – причина, более позднее – следствие.

2. Направление связи не является обратным (необходимо в связи с ошибкой ретроспективного измерения)

Направление связи не является обратным (необходимо в связи с ошибкой ретроспективного измерения)

3. Взаимосвязь (ковариация/корреляция)

Наличие взаимосвязи (ковариация)

4. Изолированность (никакая третья переменная не объясняет ковариацию)

Неизолированная

Изолированная связь

5. Известная форма распределения (детерминистское, вероятностное)

Полностью ли данный предиктор определяет зависимую переменную (детерминистское) или только какую-то небольшую ее вероятность (вероятностное)?

Детерминистское

Вероятностное

🏠 Дома:

Учебник Назарова и Мальцев: Главы 3.2, 4.6; Тема 9, Часть С.
Учебник Kline, Ch.1,6,7.

Максим Руднев, 2018-2021 на основе RMarkdown.

Лекция 4 – Введение в структурные уравнения

15 сентября 2021 г.