Конфирматорный факторный анализ
23 сентября 2021 г.
1 🕹 lavaan
1.1 Формулы
MODEL1 <-"
F1 =~ creative + be_free;
F2 =~ adventur + diff_thi # По умолчанию нагрузка первого
# индикатора фиксируется равной 1.
# Если использовать *, нагрузка следующего по
# порядку индикатора будет фиксироваться равной 1.
"
MODEL1 <-"
# Более эксплицитно:
F1 =~ 1*creative + NA*be_free + 0*adventur + 0*diff_thi;
F2 =~ 0*creative + 0*be_free + 1*adventur + NA*diff_thi
# То есть перекрестные нагрузки установлены равными нулю.
F1 ~ F2; # F1 является следствеим F2
diff_thi ~~ be_free; # остатки индикаторов скоррелированы
"
cfa(model = MODEL1,
data = PT,
estimator = "ml", # можно не включать, задается по умолчанию;
# можно поменять в случае нарушения допущений о
# нормальности распределений и интервальном
# характере шкал;
missing="listwise" # другая опция - fiml - использование
# всей имеющейся информации внутри
# алгоритма ML. Может потребовать больше
# времени на вычисление.
) 1.2 Операторы
| оператор | значение |
|---|---|
| =~ | Измерен с помощью |
| ~ | Зависит от |
| ~~ | Скоррелирован с |
| ~ 1 | Интерсепт (константа) |
| NA*x | Освобождение параметра |
| 1*х | Фиксация параметра = 1 |
| Label*x | Приписывания параметру названия. Одинаковые ярлыки уравнивают параметры |
1.3 Фиксация и освобождение параметров
F1 ~~ F2; # Разрешить факторам коррелировать (по умолчанию разрешено, можно не прописывать).
F1 ~~ 0*F2; # Запретить факторам коррелировать между собой (по умолчанию разрешено) – ортогональные факторы;
creative ~~ be_free; # Разрешить остаткам индикаторов коррелировать между собой (по умолчанию запрещено).
creative ~~ 0*be_free; # Запретить остаткам индикаторов коррелировать между собой (по умолчанию, можно не прописывать).
F1 ~~ 1*F1; # Зафиксировать дисперсию латентной переменной (фактора) равной нулю (стандартизирует параметры).2 🗜 Конфирматорный факторный анализ
Построим двух- и трехфакторные модели КФА используя оператор =~ и сравним их между собой. lavaan автоматически устанавливает факторную нагрузку равной 1 для первой наблюдаемой переменной в списке. Данный параметр становится своего рода единицей измерения фактора, его метрикой. Поэтому, в качестве переменной, у которой факторная нагрузка будет равна 1, нужно брать переменную, которая наиболее надежно отражает искомый фактор. К примеру, переменная free в нашем случае наиболее надежно отражает искомый фактор Openness. Тогда мы, прописывая код, должны установить для этой переменной нагрузку, равной 1, и, соответственно, освободить нагрузку первого индикатора в списке. Для фиксации значения факторной нагрузки используется число и звездочка 1*free, для освобождения NA*different.
library("lavaan")
cfa1 <- cfa(model = "
Openness =~ creative + free + adventures + different + good.time;
Conservation =~ follow.rules + modest + safety",
data = PT.values)Построим диаграмму двухфакторной модели, используя функцию semPaths
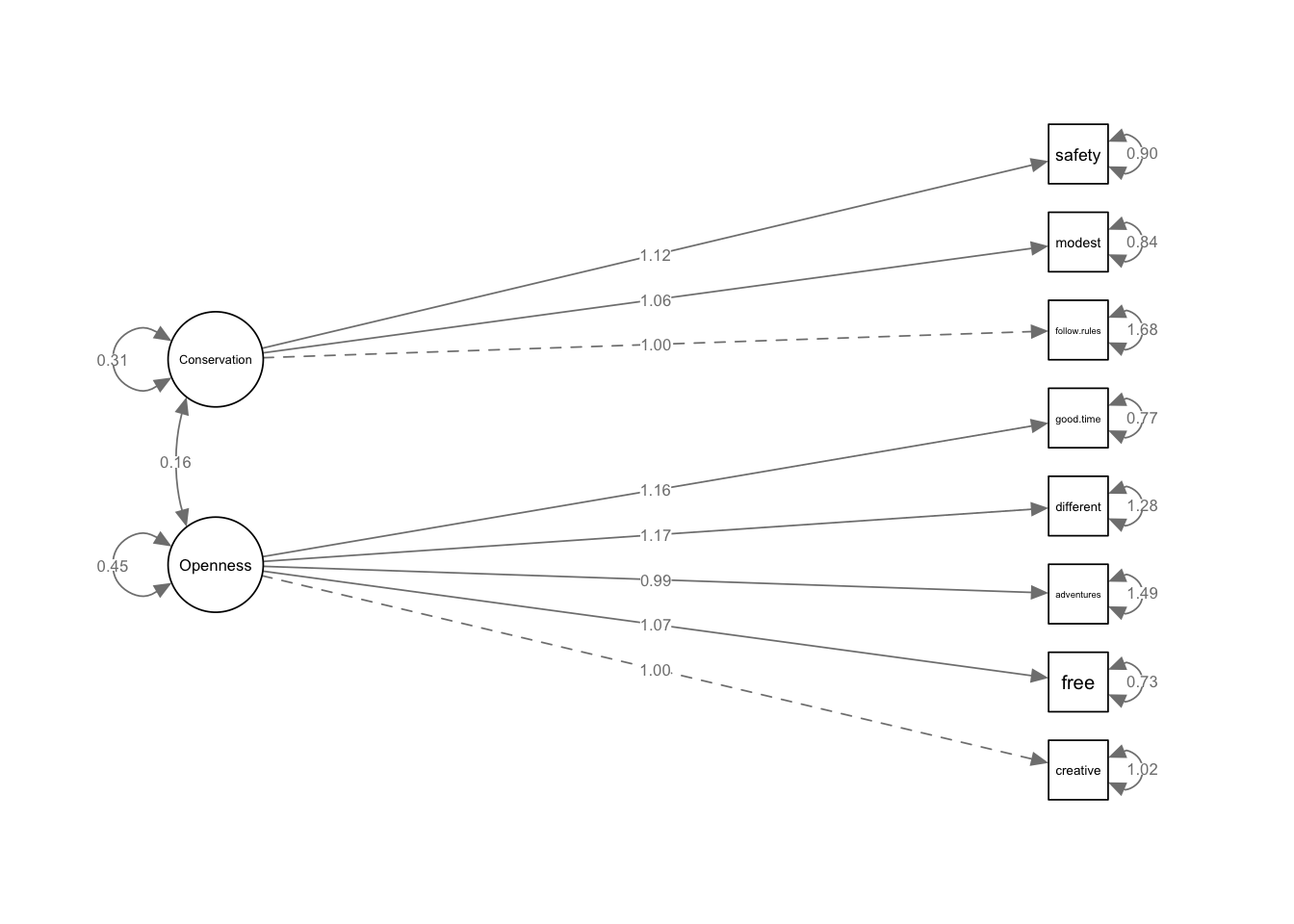
Посмотрим на статистики согласия модели с данными
> lavaan 0.6-9 ended normally after 42 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 17
>
> Used Total
> Number of observations 1207 1265
>
> Model Test User Model:
>
> Test statistic 197.373
> Degrees of freedom 19
> P-value (Chi-square) 0.000
>
> Model Test Baseline Model:
>
> Test statistic 1482.312
> Degrees of freedom 28
> P-value 0.000
>
> User Model versus Baseline Model:
>
> Comparative Fit Index (CFI) 0.877
> Tucker-Lewis Index (TLI) 0.819
>
> Loglikelihood and Information Criteria:
>
> Loglikelihood user model (H0) -15076.498
> Loglikelihood unrestricted model (H1) -14977.811
>
> Akaike (AIC) 30186.996
> Bayesian (BIC) 30273.626
> Sample-size adjusted Bayesian (BIC) 30219.627
>
> Root Mean Square Error of Approximation:
>
> RMSEA 0.088
> 90 Percent confidence interval - lower 0.077
> 90 Percent confidence interval - upper 0.100
> P-value RMSEA <= 0.05 0.000
>
> Standardized Root Mean Square Residual:
>
> SRMR 0.055
>
> Parameter Estimates:
>
> Standard errors Standard
> Information Expected
> Information saturated (h1) model Structured
>
> Latent Variables:
> Estimate Std.Err z-value P(>|z|)
> Openness =~
> creative 1.000
> free 1.071 0.074 14.400 0.000
> adventures 0.987 0.082 12.036 0.000
> different 1.172 0.087 13.512 0.000
> good.time 1.159 0.080 14.571 0.000
> Conservation =~
> follow.rules 1.000
> modest 1.059 0.137 7.728 0.000
> safety 1.122 0.145 7.716 0.000
>
> Covariances:
> Estimate Std.Err z-value P(>|z|)
> Openness ~~
> Conservation 0.163 0.025 6.481 0.000
>
> Variances:
> Estimate Std.Err z-value P(>|z|)
> .creative 1.018 0.049 20.622 0.000
> .free 0.726 0.040 18.154 0.000
> .adventures 1.489 0.068 21.959 0.000
> .different 1.282 0.063 20.253 0.000
> .good.time 0.770 0.044 17.483 0.000
> .follow.rules 1.679 0.082 20.581 0.000
> .modest 0.840 0.055 15.194 0.000
> .safety 0.903 0.061 14.807 0.000
> Openness 0.451 0.051 8.876 0.000
> Conservation 0.313 0.062 5.020 0.0002.1 Сравнение моделей
Построим трехфакторную модель и сравним ее с двухфакторной.
cfa2 <- cfa("Creativity =~ creative + free;
Stimulation =~ adventures + different + good.time;
Conservation =~ follow.rules + modest + safety",
data = PT.values)
summary(cfa2,
fit.measures = TRUE,
estimates = FALSE) # или короче summary(cfa2, fit = T, est = F) > lavaan 0.6-9 ended normally after 48 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 19
>
> Used Total
> Number of observations 1207 1265
>
> Model Test User Model:
>
> Test statistic 166.786
> Degrees of freedom 17
> P-value (Chi-square) 0.000
>
> Model Test Baseline Model:
>
> Test statistic 1482.312
> Degrees of freedom 28
> P-value 0.000
>
> User Model versus Baseline Model:
>
> Comparative Fit Index (CFI) 0.897
> Tucker-Lewis Index (TLI) 0.830
>
> Loglikelihood and Information Criteria:
>
> Loglikelihood user model (H0) -15061.204
> Loglikelihood unrestricted model (H1) -14977.811
>
> Akaike (AIC) 30160.409
> Bayesian (BIC) 30257.231
> Sample-size adjusted Bayesian (BIC) 30196.879
>
> Root Mean Square Error of Approximation:
>
> RMSEA 0.085
> 90 Percent confidence interval - lower 0.074
> 90 Percent confidence interval - upper 0.097
> P-value RMSEA <= 0.05 0.000
>
> Standardized Root Mean Square Residual:
>
> SRMR 0.051Двух- и трехфакторные модели не являются вложенными. Поэтому мы не можем провести тест разницы хи-квадратов. Но можно ориентироваться на значения BIC и AIC.
Подтверждается ли изначальная гипотеза о наличии именно двух факторов?
> Chi-Squared Difference Test
>
> Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
> cfa2 17 30160 30257 166.79
> cfa1 19 30187 30274 197.37 30.587 2 2.281e-07 ***
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 12.2 Модификационные индексы и вложенные модели
Проинтерпретируем все выведенные статистики согласия. Что же с моделью не так? Здесь могут помочь модификационные индексы.
- lhs - левая сторона
- op - оператор
- rhs - правая сторона
- mi - модификационный индекс (на сколько уменьшится хи-квадрат если добавить этот параметр в модель)
- epc - ожидаемое значение параметра
Строки с операторами
=~соответствуют факторным нагрузкам,~~соответствуют ковариации между остатками индикаторов.
modindices(cfa2,
minimum.value = 10, # не показывать индексы менее 10
sort = TRUE # отсортировать по убыванию
) lhs op rhs mi epc sepc.lv sepc.all sepc.nox
25 Creativity =~ good.time 58.372 1.947 1.368 1.166 1.166
52 adventures ~~ different 48.764 0.366 0.366 0.279 0.279
36 Conservation =~ adventures 46.662 -0.779 -0.423 -0.305 -0.305
38 Conservation =~ good.time 43.829 0.691 0.375 0.320 0.320
48 free ~~ good.time 35.611 0.219 0.219 0.323 0.323
47 free ~~ different 27.392 -0.211 -0.211 -0.244 -0.244
23 Creativity =~ adventures 25.161 -1.129 -0.793 -0.571 -0.571
62 good.time ~~ modest 23.333 0.147 0.147 0.185 0.185
56 adventures ~~ safety 19.811 -0.174 -0.174 -0.155 -0.155
57 different ~~ good.time 19.102 -0.247 -0.247 -0.260 -0.260
41 creative ~~ different 16.112 0.170 0.170 0.156 0.156
66 modest ~~ safety 14.768 -0.298 -0.298 -0.344 -0.344
Мы видим, что наибольшие значения у модификационных индексов, предлагающих дополнительные (перекрестные) нагрузки, например, самое большое значение у Creativity =~ good.time. Теоретически такая перекрестная нагрузка не вполне оправдана, т.к. ценность креативность не обязательно должна находить свое выражение в ценности хорошего проведения времени. Второй по величине модификационный индекс указывает на ковариацию остатков индикаторов adventures ~~ different. Теоретически такая ковариация оправдана. Добавим ее в модель и посмотрим как изменился хи-квадарат модели.
cfa2.1 <- cfa(" Creativity =~ creative + free;
Stimulation =~ adventures + different + good.time;
Conservation =~ follow.rules+ modest+ safety;
# добавленный параметр ковариации остатков
adventures ~~ different",
data = PT.values)
summary(cfa2.1, fit = T, est = F)> lavaan 0.6-9 ended normally after 52 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 20
>
> Used Total
> Number of observations 1207 1265
>
> Model Test User Model:
>
> Test statistic 117.770
> Degrees of freedom 16
> P-value (Chi-square) 0.000
>
> Model Test Baseline Model:
>
> Test statistic 1482.312
> Degrees of freedom 28
> P-value 0.000
>
> User Model versus Baseline Model:
>
> Comparative Fit Index (CFI) 0.930
> Tucker-Lewis Index (TLI) 0.878
>
> Loglikelihood and Information Criteria:
>
> Loglikelihood user model (H0) -15036.696
> Loglikelihood unrestricted model (H1) -14977.811
>
> Akaike (AIC) 30113.393
> Bayesian (BIC) 30215.310
> Sample-size adjusted Bayesian (BIC) 30151.782
>
> Root Mean Square Error of Approximation:
>
> RMSEA 0.073
> 90 Percent confidence interval - lower 0.061
> 90 Percent confidence interval - upper 0.085
> P-value RMSEA <= 0.05 0.001
>
> Standardized Root Mean Square Residual:
>
> SRMR 0.045Посмотрите на другие статистики согласия. Достаточно ли близка модель к данным?
Посмотрим на модификационные индексы этой модели.
- Посмотрим на модификационные индексы и примете решение о добавлении еще одного параметра в модель.
- Добавим его в модель по аналогии с предыдущим этапом.
- Если необходимо, повторим эту операцию еще раз.
Не стоит добавлять слишком много параметров, т.к. мы неизбежно подгоним модель под конкретные выборочные данные (а интерес представляют только параметры генеральной совокупности!).
cfa2.2<- cfa("Creativity =~ creative + free;
Stimulation =~ adventures + different + good.time;
Conservation =~ follow.rules + modest + safety;
adventures ~~ different;
# второй новый параметр
creative ~~ different",
data = PT.values)
summary(cfa2.2,
fit = T,
est = F # эта строка исключает из выдачи все коэффициенты
)> lavaan 0.6-9 ended normally after 54 iterations
>
> Estimator ML
> Optimization method NLMINB
> Number of model parameters 21
>
> Used Total
> Number of observations 1207 1265
>
> Model Test User Model:
>
> Test statistic 93.145
> Degrees of freedom 15
> P-value (Chi-square) 0.000
>
> Model Test Baseline Model:
>
> Test statistic 1482.312
> Degrees of freedom 28
> P-value 0.000
>
> User Model versus Baseline Model:
>
> Comparative Fit Index (CFI) 0.946
> Tucker-Lewis Index (TLI) 0.900
>
> Loglikelihood and Information Criteria:
>
> Loglikelihood user model (H0) -15024.384
> Loglikelihood unrestricted model (H1) -14977.811
>
> Akaike (AIC) 30090.768
> Bayesian (BIC) 30197.782
> Sample-size adjusted Bayesian (BIC) 30131.078
>
> Root Mean Square Error of Approximation:
>
> RMSEA 0.066
> 90 Percent confidence interval - lower 0.053
> 90 Percent confidence interval - upper 0.079
> P-value RMSEA <= 0.05 0.020
>
> Standardized Root Mean Square Residual:
>
> SRMR 0.041Поскольку модели cfa2, cfa2.1, cfa2.2 являются вложенными (мы добавляли по одному параметру в каждую следующую модель), можно сравнивать их по критерию разницы хи-квадратов (он же тест разницы правдоподобий, likelihood ratio test - LRT)
> Chi-Squared Difference Test
>
> Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
> cfa2.2 15 30091 30198 93.145
> cfa2.1 16 30113 30215 117.770 24.624 1 6.966e-07 ***
> cfa2 17 30160 30257 166.786 49.016 1 2.538e-12 ***
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# или - оформленная таблица и более полная информация
library("semTable")
library("knitr")
library("kableExtra")
comp.tab <- compareLavaan(
list(Model1 = cfa2,
Model2 = cfa2.1,
Model3 = cfa2.2),
nesting = "Model1 > Model2 > Model3",
print.results = FALSE)
ktab <- knitr::kable(comp.tab)
kableExtra::kable_styling(ktab)| chisq | df | pvalue | rmsea | cfi | tli | srmr | aic | bic | dchi | ddf | npval | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model1 | 166.786 | 17 | 0 | 0.085 | 0.897 | 0.830 | 0.051 | 30160.41 | 30257.23 |
|
|
|
| Model2 | 117.770 | 16 | 0 | 0.073 | 0.930 | 0.878 | 0.045 | 30113.39 | 30215.31 | 49.016a | 1 | 0 |
| Model3 | 93.145 | 15 | 0 | 0.066 | 0.946 | 0.900 | 0.041 | 30090.77 | 30197.78 | 24.624b | 1 | 0 |
Результаты показывают, что хи-квадрат в каждой следующей модели значимо уменьшался, то есть добавление ковариаций остатков приводило к более высокому соответствию между моделью и данными. Из этого можно сделать вывод, что модель cfa2.2 лучше всего подходит к данным.
2.3 Оформление КФА
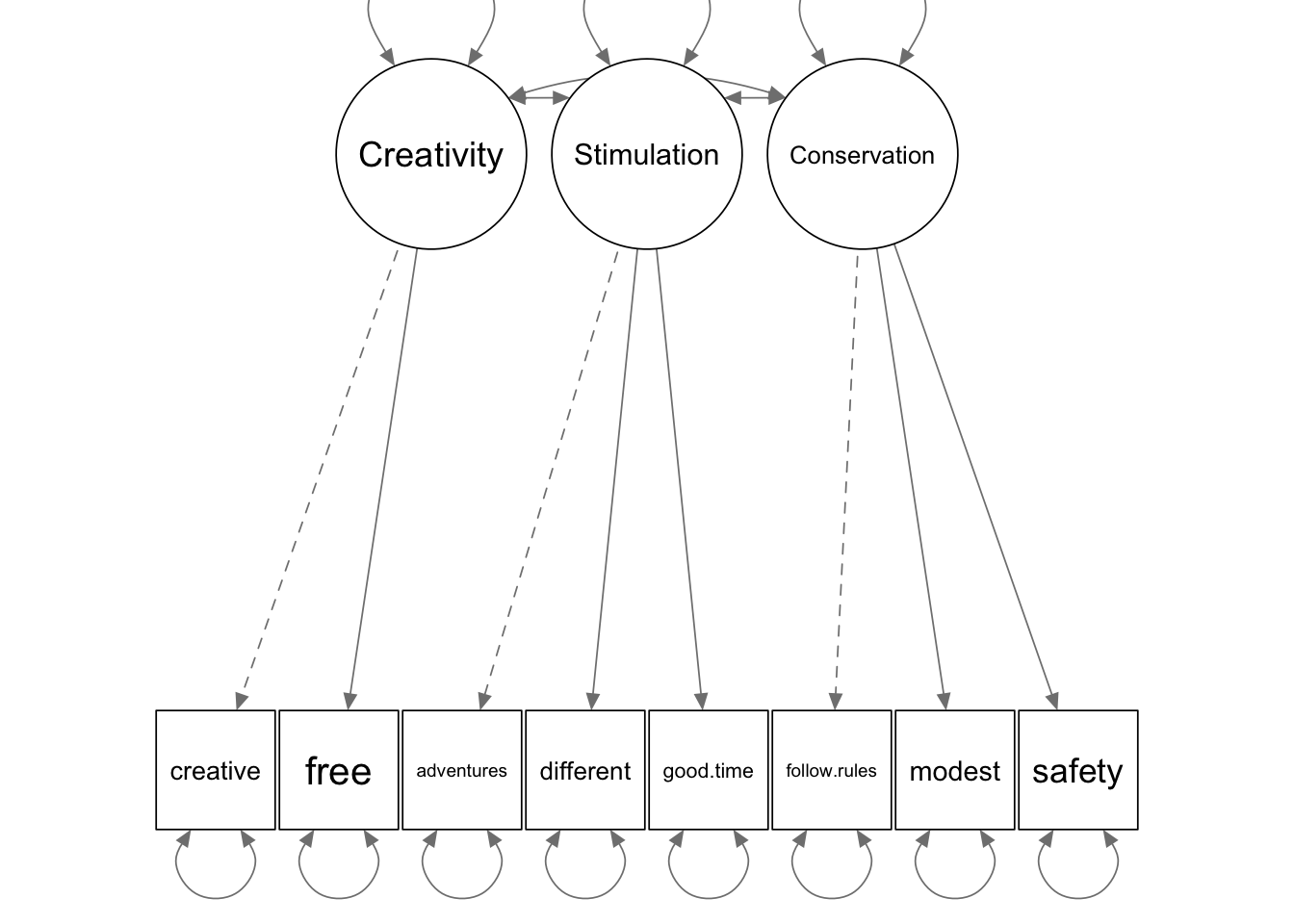
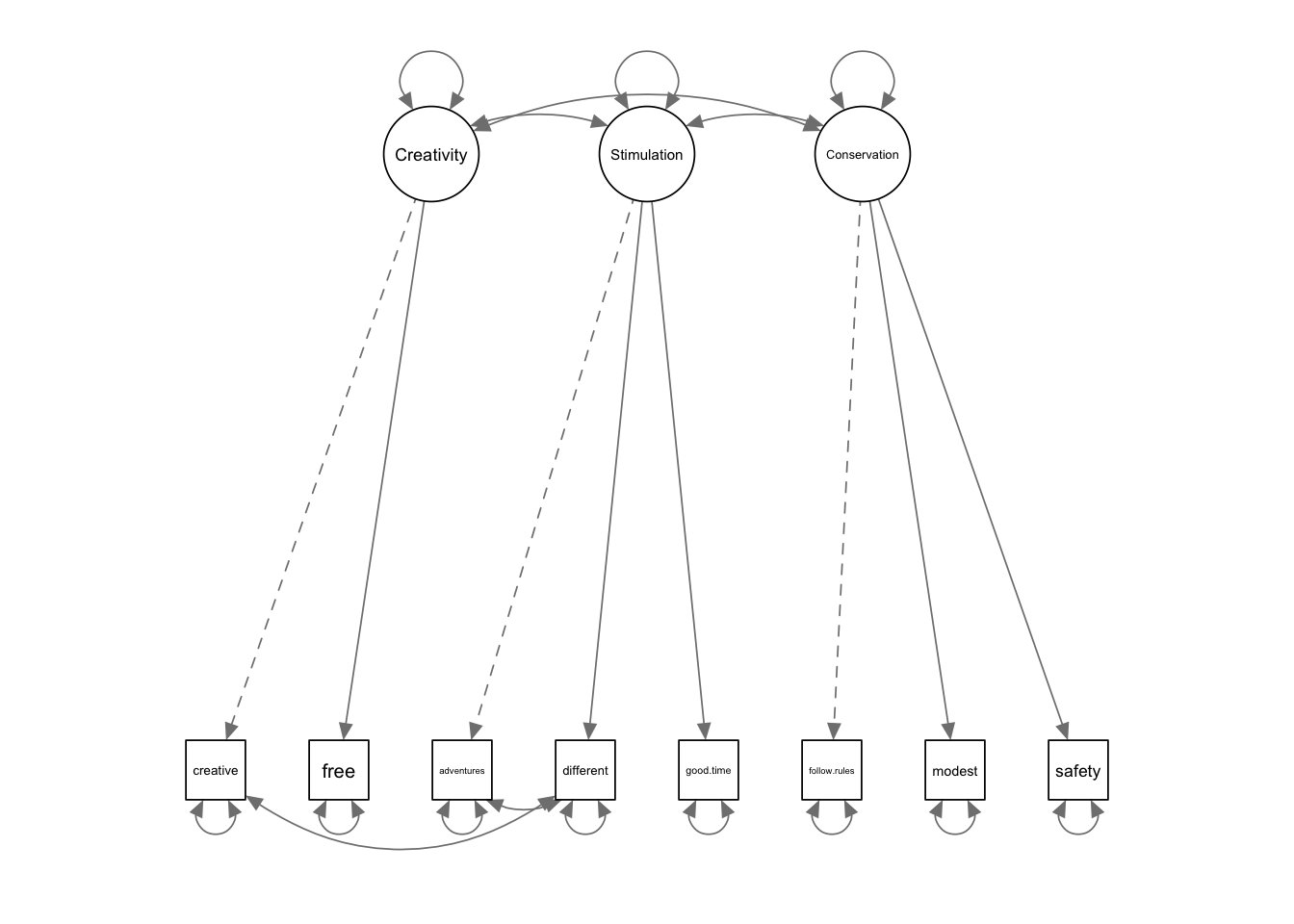
2.3.1 Диаграммы теоретической и итоговой моделей
2.3.2 Параметры моделей
library("htmltools")
last.model.tab <- semTable(list(Model1 = cfa2,
Model2 = cfa2.1,
Model3 = cfa2.2),
columns = "estsestars", # коэфф, стд.ош., звезды
type = "html", # тип таблицы
print.results = FALSE # не показывать ничего в консоли
)| Model1 | Model2 | Model3 | |
| Estimate(Std.Err.) | Estimate(Std.Err.) | Estimate(Std.Err.) | |
| Factor Loadings | |||
| Creativity | |||
| creative | 1.00+ | 1.00+ | 1.00+ |
| free | 1.13(0.08)*** | 1.21(0.09)*** | 1.34(0.11)*** |
| Stimulation | |||
| adventures | 1.00+ | 1.00+ | 1.00+ |
| different | 1.16(0.09)*** | 1.22(0.10)*** | 1.17(0.10)*** |
| good.time | 1.11(0.08)*** | 1.45(0.13)*** | 1.57(0.15)*** |
| Conservation | |||
| follow.rules | 1.00+ | 1.00+ | 1.00+ |
| modest | 1.08(0.14)*** | 1.11(0.14)*** | 1.15(0.15)*** |
| safety | 1.18(0.15)*** | 1.17(0.15)*** | 1.17(0.15)*** |
| Residual Variances | |||
| creative | 0.98(0.05)*** | 1.01(0.05)*** | 1.05(0.05)*** |
| free | 0.62(0.05)*** | 0.57(0.05)*** | 0.50(0.06)*** |
| adventures | 1.42(0.07)*** | 1.58(0.07)*** | 1.60(0.07)*** |
| different | 1.21(0.06)*** | 1.39(0.07)*** | 1.43(0.07)*** |
| good.time | 0.75(0.05)*** | 0.65(0.06)*** | 0.56(0.06)*** |
| follow.rules | 1.70(0.08)*** | 1.70(0.08)*** | 1.71(0.08)*** |
| modest | 0.84(0.05)*** | 0.83(0.05)*** | 0.82(0.05)*** |
| safety | 0.89(0.06)*** | 0.90(0.06)*** | 0.91(0.06)*** |
| Residual Covariances | |||
| adventures w/different | 0.36(0.05)*** | 0.37(0.05)*** | |
| creative w/different | 0.20(0.04)*** | ||
| Latent Variances | |||
| Creativity | 0.49(0.06)*** | 0.46(0.05)*** | 0.41(0.05)*** |
| Stimulation | 0.51(0.06)*** | 0.35(0.06)*** | 0.33(0.05)*** |
| Conservation | 0.30(0.06)*** | 0.29(0.06)*** | 0.28(0.06)*** |
| Latent Covariances | |||
| Creativity w/Stimulation | 0.42(0.04)*** | 0.34(0.04)*** | 0.29(0.04)*** |
| Creativity w/Conservation | 0.18(0.03)*** | 0.17(0.03)*** | 0.16(0.03)*** |
| Stimulation w/Conservation | 0.14(0.03)*** | 0.14(0.02)*** | 0.13(0.02)*** |
| Fit Indices | |||
| χ2 | 166.79(17)*** | 117.77(16)*** | 93.15(15)*** |
| CFI | 0.90 | 0.93 | 0.95 |
| TLI | 0.83 | 0.88 | 0.90 |
| RMSEA | 0.09 | 0.07 | 0.07 |
| +Fixed parameter | |||
| *p<0.05, **p<0.01, ***p<0.001 | |||
3 👉 Самостоятельное задание
На основе ваших результатов разведывательного факторного анализа в Германии (прошлый семинар), постройте конфирматорный факторный анализ на данных Австрии.
Начнем с формулировки гипотез о факторах: ценности жителей Австрии можно описать ## латентными переменными, которые выражаются в наблюдаемых переменных. Фактор 1 находит отражение в индикаторах … и …; фактор 2 отражается в индикаторах …
Постройте модели с разным количеством факторов. Модифицируйте их. Сравните согласие получившихся моделей.